Cechy ruchu drgającego
Przykładem ruchu drgającego może być ruch obciążnika doczepionego do sprężyny lub kulki zawieszonej na nici (wahadło).
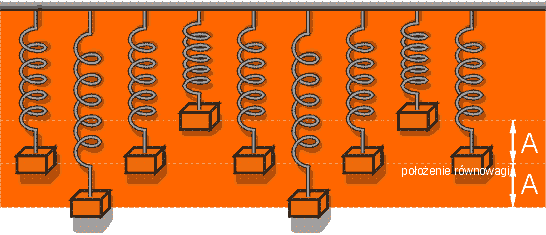
Rysunki pokazują kolejne położenia obciążnika (kulki) w czasie ruchu.
Ciało wykonujące drgania zmienia swe położenie odchylając się od położenia równowagi raz w jedną, a raz w drugą stronę. Ruch odbywa się stale na tej samej drodze i jest cyklicznym (okresowym). Czas powtarzalności jest nazywany okresem.
Opis ruchu drgającego (prostego - bez oporów)
Do opisu ruchu drgającego używamy pojęć:
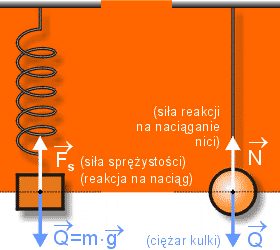
b) wychylenie (x), to odległość ciała (punktu) drgającego od położenia równowagi. Jest ono zmienne (okresowo) w czasie.
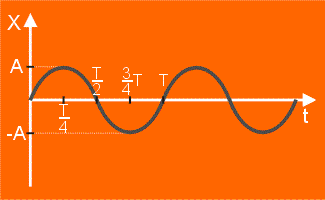
Zależność (położenia) wychylenia od czasu obrazuje powyższy wykres. Jego przebieg jest podobny do wykresu sina , a różni się od niego wartościami maksymalnymi.
A jest największym możliwym wychyleniem. Największe wychylenie ciała z położenia równowagi nazywamy amplitudą.
xmax= A
W dowolnym momencie trwania ruchu wychylenie wynosi:
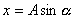
gdzie a to tzw. faza ruchu i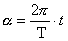 czyli
czyli 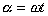 (w - prędkość kątowa), a T to okres drgań, np. gdy t =
(w - prędkość kątowa), a T to okres drgań, np. gdy t = 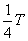 to
to 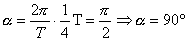 i
i 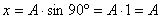
c) okres (T) i częstotliwość (f) drgań
Okres, to czas powtarzalności. Jest to czas w którym ciało (punkt) wykona jedno pełne drganie (czyli odbędzie ruch np. od położenia równowagi do maksymalnego wychylenia, zawróci, przejdzie przez położenia równowagi do maksymalnego wychylenia w drugą stronę znów zawróci i dojdzie do położenia równowagi). Okres drgań oznaczamy literą T i wyrażamy w jednostkach czasu czyli sekundach. W czasie 1T ciało przebywa drogę równą 4A.
Odwrotność okresu (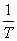 ) jest miarą częstotliwości drgań.
) jest miarą częstotliwości drgań.
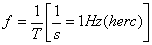
Częstotliwość to liczba drgań wykonanych w czasie jednej sekundy. Okres drgań ( i częstotliwości) zależy od właściwości sprężyny do której jest doczepiony obciążnik
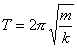
m jest masa drgającą ciała (punktu), a k - współczynnik sprężystości sprężyny.
d) prędkość
Prędkość ciała (punktu) drgającego nie jest stała w czasie. Ruch drgający jest ruchem niejednostajnie opóźnionym przy wzroście wychylenia, a jednocześnie przyspieszonym przy zmniejszaniu się wychylenia. Gdy wychylenie wynosi zero(ciało przechodzi przez położenie równowagi) prędkość wynosi 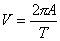 i jest ona maksymalna. Gdy wychylenie
i jest ona maksymalna. Gdy wychylenie
jest maksymalne (A) prędkość wynosi zero (moment zawracania).
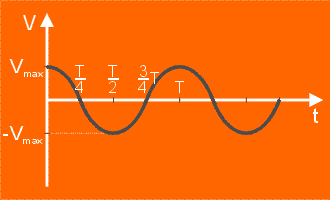
Zależność prędkości od czasu przedstawia wykres. Przypomina on przebieg zmienności funkcji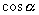 .
.
W dowolnym momencie trwania ruchu prędkość ciała drgającego wynosi:
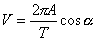 , gdzie
, gdzie 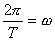 a faza
a faza 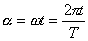 np.:
np.:
gdy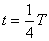 to
to 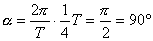 i
i 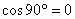 zatem V= 0
zatem V= 0
e) przyspieszenie i siła
Ruch drgający nie jest jednostajnie zmienny, więc ciało drgające doznaje przyspieszenia (a) zmiennego w czasie. Przyspieszenie jest proporcjonalne do wychylenia (w tych samych momentach = a = 0 gdy x = 0 i a = a max gdy x = A), ale zwrot przyspieszenia jest przeciwny do wychylenia. Przyspieszenie jest w każdym momencie ruchu zwrócone w stronę położenia równowagi.
Przyspieszenie punktu drgającego można obliczyć z równania:
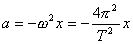
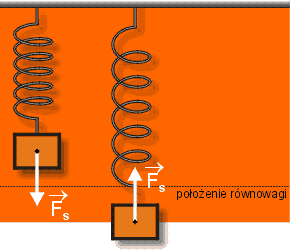
Przyspieszenie jest skutkiem działania siły sprężystości (siły dążącej do przywrócenia stanu równowagi). Tę siłę wyrażamy na podtawie II zasady dynamiki :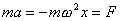
Jest ona proporcjonalna do wychylenia (gdy x rośnie, to F też rośnie) i zwrócona przeciwnie do wychylenia (zawsze do położenia równowagi)
Wyrażenie : mw2 = k jest współczynnikiem sprężystości, więc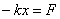
f) energia i jej przemiany
Ciała poruszające się posiadają energię kinetyczną, zatem punkt drgający posiada energię kinetyczną, której wartość:
Energia kinetyczna zmienia się w czasie, gdyż prędkość ciała nie jest stała . Gdy prędkość ciała maleje, rośnie jego wychylenie i energia kinetyczna ulega przemianie w energię potencjalną (sprężystości):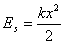
W dowolnym momencie trwania ruchu energia jest równa sumie energii kinetycznej i potencjalnej ma ona wartość:
Ponieważ k (współczynnik sprężystości) i A (amplituda drgań) są dla danego ciała stałe więc energia ciała drgającego jest stała. Ulega ona przemianie tzn. Ek zamienia się w Es- i na odwrót Es zamienia się w Ek.
Gdy x = 0, v = vmax i ciało ma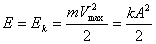 ; gdy x = A, ciało ma v = 0 i
; gdy x = A, ciało ma v = 0 i 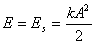
Wahadło (okres drgań)
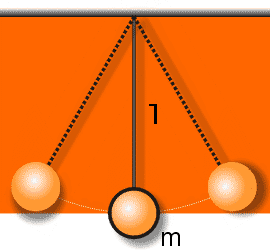
Wahadło stanowić może każde ciało zawieszone na np. nici i wytrącone z położenia równowagi. Idealne wahadło stanowi tzw. wahadło matematyczne. Jest nim ciało o masie m skupionej w jednym punkcie, zawieszone na nierozciągliwej i nieważkiej nici:
Okres drgań takiego wahadła nie zależy ani od masy ani do amplitudy drgań (jeśli ciało ma małe rozmiary (jest punktowe) i odchylenia od równowagi są małe). Okres drgań zależy od długości nici i wyraża się wzorem: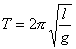
(l jest długością wahadła a g przyspieszeniem grawitacyjnym)
Częstotliwość drgania wahadła :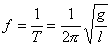
Wahadło można wykorzystać do wyznaczania wartości przyspieszenia grawitacyjnego poprzez: pomiar czasu (t) trwania dowolnie dużej liczby(n) drgań (im więcej, tym dokładniejszy pomiar) w celu wyznaczenia okresu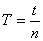 i pomiar długości (l) nici:
i pomiar długości (l) nici:
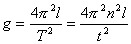
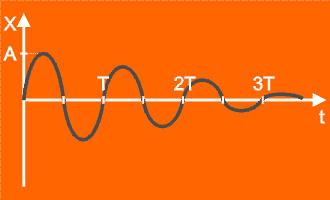
Drgania gasnące i wymuszone
Ciało drgające napotyka na np. opór ośrodka. Siły opory powodują tłumienie drgań (część energii zostaje zużyta na wykonanie przez ciało pracy przeciwko siłom oporu). Amplituda takich drgań maleje.
Takie drgania nazywamy tłumionymi (również gasnącymi).
Aby zapobiec wygasaniu drgań należy sysytematycznie uzupełniać ubytki energii poprzez okresowe działanie sił. Takie drgania nazywamy wymuszonymi np. huśtawka - utrzymanie jednakowych wychyleń wymaga dodatkowych, rytmicznych działań.
Każde ciało można pobudzić do drgań poprzez przekazywanie mu energii innego ciała, pod warunkiem, że okresy drgań obu ciał są takie same. Taki proces nazywamy rezonansem.
Przykład rezonansu przedstawia rysunek:
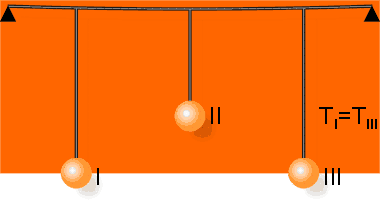
Gdy wahadło I zostanie wprowadzone w ruch, jego drgania zostaną przekazane (poprzez więzy) do wahadła III. Wahadła I i III będą równocześnie wykonywać drgania o zmieniających się amplitudach tak, że gdy AI = max to AIII = 0; gdy AI = 0 to AIII = max.
Zjawisko rezonansu może stać się przyczyną rozerwania np. mostu czy stropu hali fabrycznej gdy zostaną pobudzone do drgań, których amplituda będzie tak duża, iż przekroczone zostaną granice wytrzymałości na rozerwanie.
Przykładem ruchu drgającego może być ruch obciążnika doczepionego do sprężyny lub kulki zawieszonej na nici (wahadło).

Rysunki pokazują kolejne położenia obciążnika (kulki) w czasie ruchu.
Ciało wykonujące drgania zmienia swe położenie odchylając się od położenia równowagi raz w jedną, a raz w drugą stronę. Ruch odbywa się stale na tej samej drodze i jest cyklicznym (okresowym). Czas powtarzalności jest nazywany okresem.
Opis ruchu drgającego (prostego - bez oporów)
Do opisu ruchu drgającego używamy pojęć:
- położenie równowagi
- wychylenie i amplituda
- okres i częśtotliwość ruchu
- prędkość
- przyspieszenie i siła
- energia i przemiany energii

b) wychylenie (x), to odległość ciała (punktu) drgającego od położenia równowagi. Jest ono zmienne (okresowo) w czasie.

Zależność (położenia) wychylenia od czasu obrazuje powyższy wykres. Jego przebieg jest podobny do wykresu sina , a różni się od niego wartościami maksymalnymi.
A jest największym możliwym wychyleniem. Największe wychylenie ciała z położenia równowagi nazywamy amplitudą.
xmax= A
W dowolnym momencie trwania ruchu wychylenie wynosi:
gdzie a to tzw. faza ruchu i
c) okres (T) i częstotliwość (f) drgań
Okres, to czas powtarzalności. Jest to czas w którym ciało (punkt) wykona jedno pełne drganie (czyli odbędzie ruch np. od położenia równowagi do maksymalnego wychylenia, zawróci, przejdzie przez położenia równowagi do maksymalnego wychylenia w drugą stronę znów zawróci i dojdzie do położenia równowagi). Okres drgań oznaczamy literą T i wyrażamy w jednostkach czasu czyli sekundach. W czasie 1T ciało przebywa drogę równą 4A.
Odwrotność okresu (
Częstotliwość to liczba drgań wykonanych w czasie jednej sekundy. Okres drgań ( i częstotliwości) zależy od właściwości sprężyny do której jest doczepiony obciążnik
m jest masa drgającą ciała (punktu), a k - współczynnik sprężystości sprężyny.
d) prędkość
 |
||
| prędkość |
jest maksymalne (A) prędkość wynosi zero (moment zawracania).
Zależność prędkości od czasu przedstawia wykres. Przypomina on przebieg zmienności funkcji
W dowolnym momencie trwania ruchu prędkość ciała drgającego wynosi:
gdy
e) przyspieszenie i siła
 |
||
| siła sprężystości |
Przyspieszenie punktu drgającego można obliczyć z równania:
Przyspieszenie jest skutkiem działania siły sprężystości (siły dążącej do przywrócenia stanu równowagi). Tę siłę wyrażamy na podtawie II zasady dynamiki :
Jest ona proporcjonalna do wychylenia (gdy x rośnie, to F też rośnie) i zwrócona przeciwnie do wychylenia (zawsze do położenia równowagi)
Wyrażenie : mw2 = k jest współczynnikiem sprężystości, więc
f) energia i jej przemiany
Ciała poruszające się posiadają energię kinetyczną, zatem punkt drgający posiada energię kinetyczną, której wartość:
Energia kinetyczna zmienia się w czasie, gdyż prędkość ciała nie jest stała . Gdy prędkość ciała maleje, rośnie jego wychylenie i energia kinetyczna ulega przemianie w energię potencjalną (sprężystości):
W dowolnym momencie trwania ruchu energia jest równa sumie energii kinetycznej i potencjalnej ma ona wartość:
Ponieważ k (współczynnik sprężystości) i A (amplituda drgań) są dla danego ciała stałe więc energia ciała drgającego jest stała. Ulega ona przemianie tzn. Ek zamienia się w Es- i na odwrót Es zamienia się w Ek.
Gdy x = 0, v = vmax i ciało ma
Wahadło (okres drgań)
 |
||
| wahadło |
Okres drgań takiego wahadła nie zależy ani od masy ani do amplitudy drgań (jeśli ciało ma małe rozmiary (jest punktowe) i odchylenia od równowagi są małe). Okres drgań zależy od długości nici i wyraża się wzorem:
(l jest długością wahadła a g przyspieszeniem grawitacyjnym)
Częstotliwość drgania wahadła :
Wahadło można wykorzystać do wyznaczania wartości przyspieszenia grawitacyjnego poprzez: pomiar czasu (t) trwania dowolnie dużej liczby(n) drgań (im więcej, tym dokładniejszy pomiar) w celu wyznaczenia okresu
Drgania gasnące i wymuszone
Ciało drgające napotyka na np. opór ośrodka. Siły opory powodują tłumienie drgań (część energii zostaje zużyta na wykonanie przez ciało pracy przeciwko siłom oporu). Amplituda takich drgań maleje.
Takie drgania nazywamy tłumionymi (również gasnącymi).

Aby zapobiec wygasaniu drgań należy sysytematycznie uzupełniać ubytki energii poprzez okresowe działanie sił. Takie drgania nazywamy wymuszonymi np. huśtawka - utrzymanie jednakowych wychyleń wymaga dodatkowych, rytmicznych działań.
Każde ciało można pobudzić do drgań poprzez przekazywanie mu energii innego ciała, pod warunkiem, że okresy drgań obu ciał są takie same. Taki proces nazywamy rezonansem.
Przykład rezonansu przedstawia rysunek:

Gdy wahadło I zostanie wprowadzone w ruch, jego drgania zostaną przekazane (poprzez więzy) do wahadła III. Wahadła I i III będą równocześnie wykonywać drgania o zmieniających się amplitudach tak, że gdy AI = max to AIII = 0; gdy AI = 0 to AIII = max.
Zjawisko rezonansu może stać się przyczyną rozerwania np. mostu czy stropu hali fabrycznej gdy zostaną pobudzone do drgań, których amplituda będzie tak duża, iż przekroczone zostaną granice wytrzymałości na rozerwanie.