Fourier: Konstruowanie fal

Zagadnienia

• Szereg Fouriera
• Dźwięk
• Składowe harmoniczne
• Paczki falowe
• Zasada nieoznaczoności
• Funkcje trygonometryczne

Opis

Dowiedz się, jak tworzyć fale o różnych kształtach, dodając sinusy lub cosinusy. Twórz fale w przestrzeni i czasie oraz mierz ich długości i okresy. Zobacz, jak zmiana amplitud różnych składowych harmonicznych zmienia fale. Porównaj różne wyrażenia matematyczne opisujące fale.

PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu Na licencji CC BY 4.0

W opracowaniu niniejszego poradnika wykorzystano materiały PhET: Strona źródłowa symulacji, Teacher Tips (Rouinfar, listopad 2021)

W szablonie strony wykorzystano kod html/css: phydemo.app.

Poziom

Szkoła średnia

Przykładowe cele nauczania

• Wyjaśnij jakościowo, jak sinusy i cosinusy sumują się, tworząc dowolne funkcje okresowe.
• Zauważ, że każda składowa Fouriera odpowiada fali sinusoidalnej o innej długości fali lub okresie.
• Opisuj dźwięki w kategoriach fal sinusoidalnych.
• Porównaj i skontrastuj fale w przestrzeni i fale w czasie.
• Rozpoznaj, że długość fali i okres nie odpowiadają konkretnym punktom na wykresie, ale wskazują długość/czas pomiędzy dwoma kolejnymi minimami, maksimami lub innymi odpowiadającymi (ta sama faza) sobie punktami.
• Odnieś zapis matematyczny szeregu Fouriera do jego graficznej reprezentacji i określ, który aspekt wykresu jest opisany przez każdy z symboli w równaniu.
• Zauważ, że λ i T oraz k i ω to wielkości analogiczne, ale nie takie same.
• Przepisz równanie z zapisu sumarycznego na zapis rozszerzony.
• Dostrzeż, że szerokość paczki falowej w przestrzeni położenia jest odwrotnie związana z szerokością paczki falowej w przestrzeni Fouriera.
• Wyjaśnij, jak z własności fal wynika zasada nieoznaczoności Heisenberga.
• Rozpoznaj, że odstęp między składowymi Fouriera jest odwrotnie proporcjonalny do odstępu między paczkami falowymi oraz że ciągły rozkład składowych Fouriera prowadzi do pojedynczej paczki falowej.

Przykładowe materiały teoretyczne

• Szereg Fouriera (Wikipedia)
• Transformacje Fouriera (AGH)
• Interaktywny wstęp do transformaty Fouriera (Jez Swanson)

Sterowanie symulacją

Ekran Forma dyskretna (link bezpośredni)

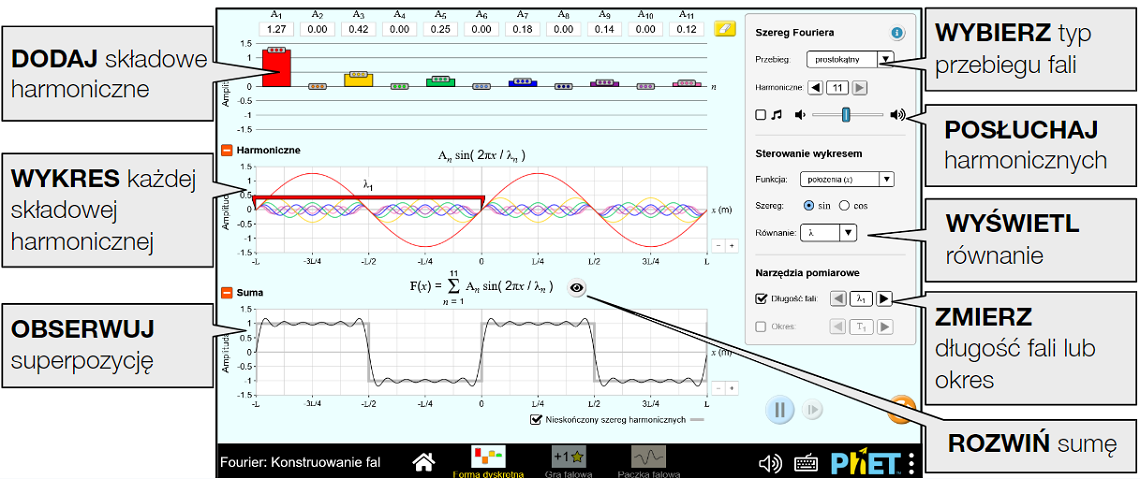
Sumuj sinusy i cosinusy, aby tworzyć fale o różnych kształtach. Odkryj, jak zmiana amplitudy różnych składowych harmonicznych zmienia dźwięk, który słyszysz.

Ekran Gra falowa (link bezpośredni)

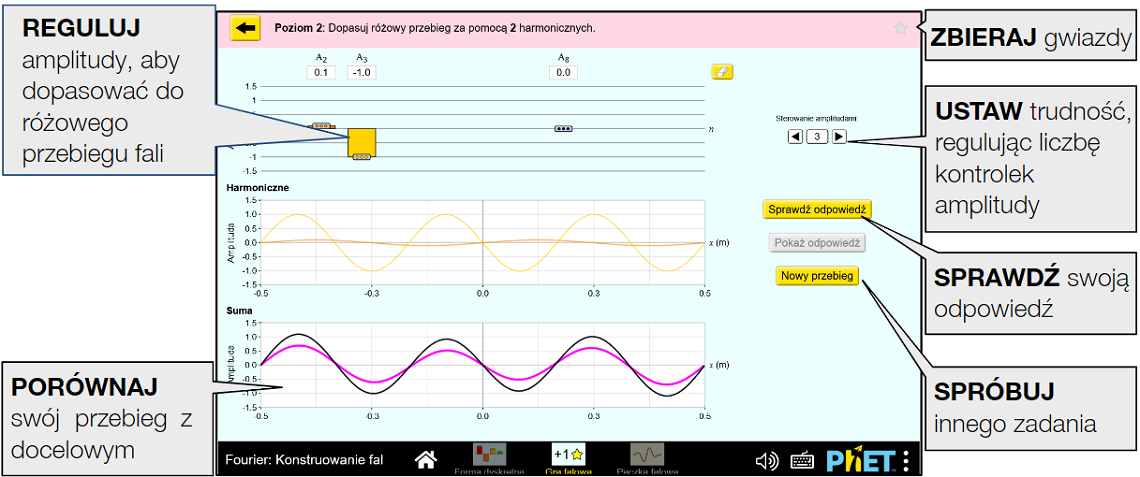
Łączenie składowych harmonicznych w celu dopasowania do docelowego przebiegu fali. Ustaw liczbę regulatorów amplitudy, aby dostosować poziom trudności.

Kontrola skomplikowania

• Trudność gry można regulować, ustawiając liczbę kontrolek amplitudy. Minimalna wartość to liczba niezerowych składowych harmonicznych. Zwiększenie tej wartości spowoduje losowe dodanie suwaków amplitudy odpowiadających składowym harmonicznym, które nie mają wpływu na różowy kształt fali.
• Najechanie kursorem myszy na jeden z suwaków amplitudy, narzędzie długości fali lub narzędzie okresu powoduje podświetlenie odpowiedniej składowej harmonicznej na wykresie harmonicznych.

Ekran Paczka falowa (link bezpośredni)

Konstruowanie paczek falowych i badanie efektów zmiany rozstawu składowych Fouriera i szerokości paczki falowej.

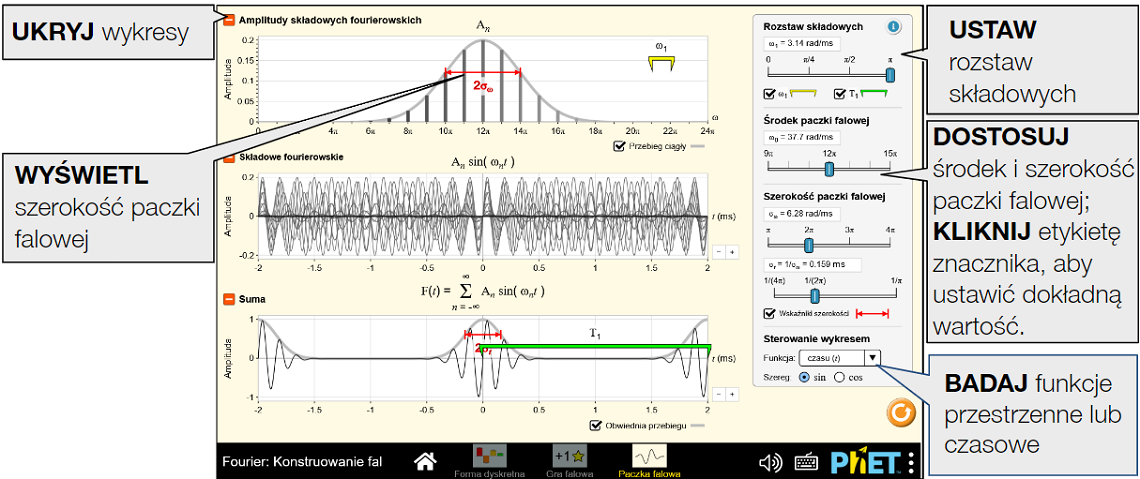
Opcje dostosowywania

Poniższe parametry query umożliwiają dostosowanie symulacji i można je dodać, dołączając znak '?' do adresu URL symulacji i oddzielając każdy parametr query znakiem '&'. Ogólny wzorzec adresu URL to: …html?queryParameter1&queryParameter2&queryParameter3

Na przykład, jeśli w symulacji Fourier: Konstruowanie fal chcesz zmienić kolejność ekranów (screens=2,1), z domyślnie otwartym drugim ekranem (initialScreen=2), użyj: https://www.edukator.pl/simulations/fourier-making-waves_all.html?screens=1,2&initialScreen=2

Aby uruchomić to w języku polskim (locale=pl), adres URL będzie wyglądał następująco: https://www.edukator.pl/simulations/fourier-making-waves_all.html?locale=pl&screens=1,2&initialScreen=2

Parametr query i opis	Przykłady
gameLevels - określa, które poziomy pojawią się w grze.	gameLevels=1,2,3
rewardScore - ustawia liczbę zadań, które należy ukończyć przed przejściem do kolejnego poziomu (domyślnie 5).	rewardScore=3
screens - określa, które ekrany są włączone do symulacji i jaka jest ich kolejność. Każdy ekran powinien być oddzielony przecinkiem. Więcej informacji można znaleźć w Centrum pomocy.	screens=1,2 screens=3
initialScreen - otwiera kartę SIM bezpośrednio na określonym ekranie, z pominięciem ekranu głównego.	initialScreen=1 initialScreen=2
locale - określa język symulacji przy użyciu kodów ISO 639-1. Dostępne wersje językowe można znaleźć na stronie symulacji w zakładce Tłumaczenia. Uwaga: działa to tylko wtedy, gdy adres URL symulacji kończy się na “_all.html”.	locale=pl (polski) locale=fr (francuski)
audio - jeśli muted, dźwięk jest domyślnie wyciszony. Jeśli disabled, cały dźwięk jest trwale wyłączony. (nie powoduje to usunięcia elementów sterujących dźwiękiem na ekranie - w tym drugim przypadku pozostają one nieaktywne)	audio=muted audio=disabled
allowLinks - jeśli false, wyłącza linki, które prowadzą uczniów do zewnętrznego adresu URL. Domyślnie jest true.	allowLinks=false
supportsPanAndZoom - gdy true, umożliwia przesuwanie i powiększanie symulacji za pomocą pinch-to-zoom lub elementów sterujących zoomem przeglądarki.	supportsPanAndZoom=false

Ułatwienia dostępu

Sterowanie za pomocą klawiatury - skróty klawiszowe

Generalnie sterujemy symulacją za pomocą myszy lub dotyku. Alternatywnie uczniowie mogą też nawigować i sterować elementami interaktywnymi za pomocą klawiatury. Po kliknięciu otworzy się okno z listą obsługiwanych skrótów.

Przy aktywnym ekranie Forma dyskretna lub Paczka falowa:

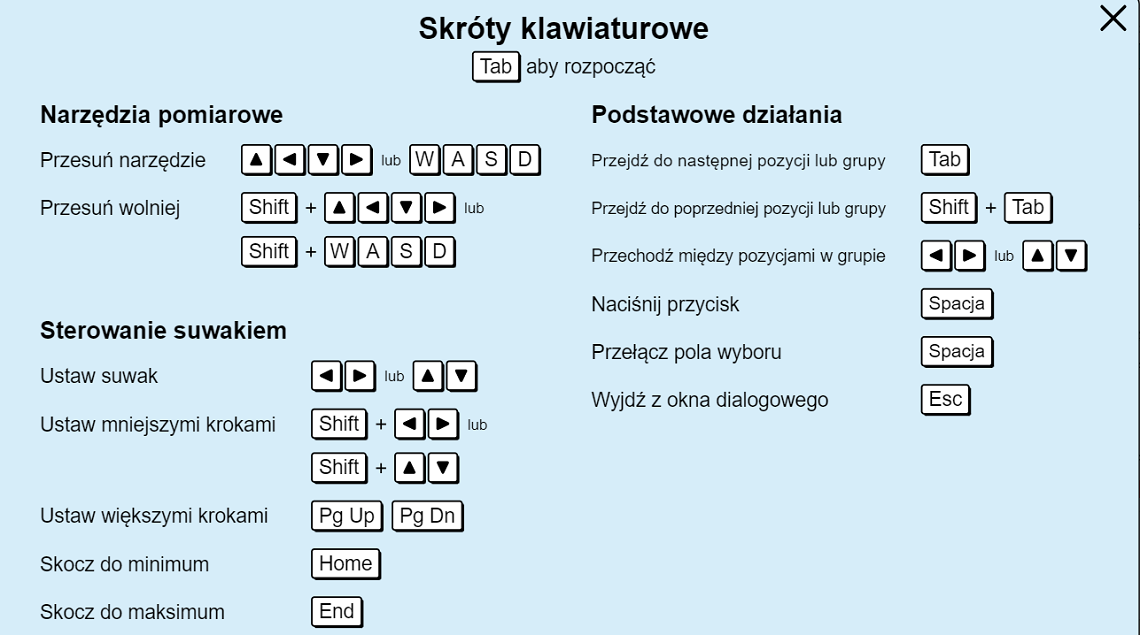
Przy aktywnym ekranie Gra falowa:

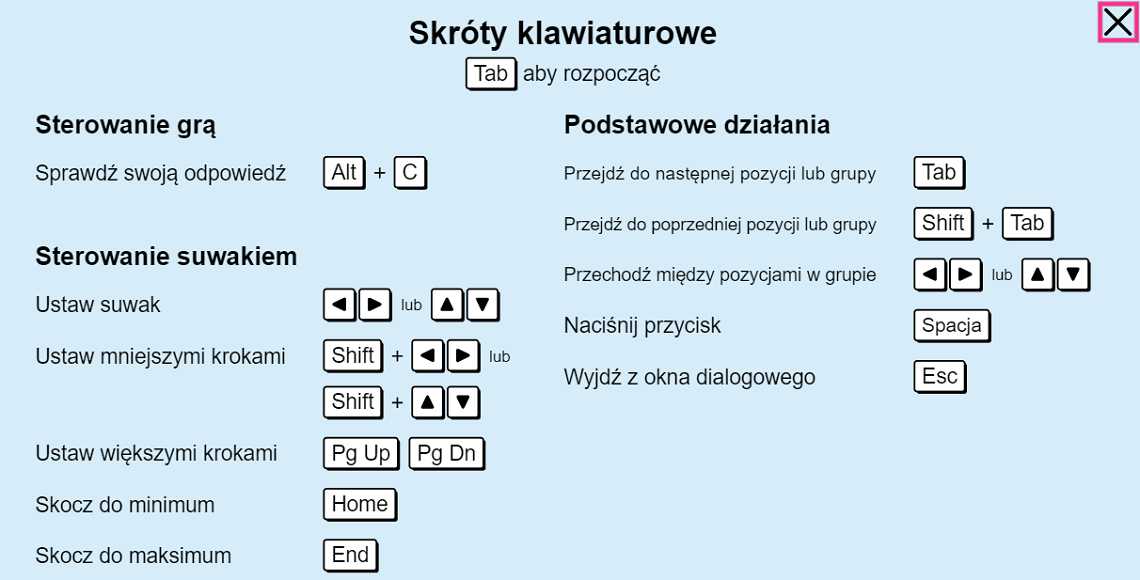
Tryb pełnoekranowy

Po kliknięciu logo PhET (na dole po prawej) pojawia się okno zawierające informacje dotyczące symulacji. Możemy tu zmienić sposób jej wyświetlania.

Klikając Pełny ekran przechodzimy do trybu pełnoekranowego (powrót - klawisz escape).

Wersje offline, niewymagające połączenia z internetem

Dostępne są również wersje symulacji niewymagające połączenia z internetem.

Aplikacja PhET Desktop zawiera wszystkie symulacje HTML5 i Java, w tym ich tłumaczenia, do użytku offline w systemach Windows i macOS (dostępne po zalogowaniu tu). Symulacje HTML5 nie wymagają dodatkowego oprogramowania, natomiast do uruchamiania dowolnych symulacji Java w aplikacji komputerowej jest wymagany Java SE Development Kit 8.

Za symboliczną opłatą możemy pobrać w postaci jednej aplikacji wszystkie materiały PhET, które zostały opublikowane w html5. Telefony, tablety i Chromebooki (z systemem Android): Google Play. iPhone'y i iPady (aplikacja na iOS): App Store

Darmową wersję desktopową tej aplikacji pobierzemy bezpośrednio klikając tu - wersja _pl zawiera polską (domyślną) i angielską wersję językową i tu - wersja _all zawiera angielską (domyślną) i wszystkie inne dostępne wersje językowe lub ze strony PhET (klikając przycisk ze strzałką przy wybranej wersji językowej):

Funkcje dźwiękowe

Dźwięk i sonifikacja

• Zaznacz pole wyboru nuta muzyczna, aby dodać sonifikację do składowych harmonicznych kształtu fali.
• Każda wyższa składowa harmoniczna ma wyższą wysokość niż poprzednia. Dlaczego tak się dzieje?
• Zwiększenie amplitudy składowej harmonicznej zwiększa również głośność jej tonu.
• Jeśli w dowolnym momencie chcesz wstrzymać sonifikację, wyłącz pole wyboru dźwięku lub całkowicie wyłącz dźwięk w symulacji za pomocą przełącznika Wszystkie dźwięki na pasku nawigacyjnym u dołu symulacji.
• Więcej przydatnych wskazówek na temat tego, jak pojęcia i dźwięki są łączone w tej symulacji, można znaleźć w filmie Funkcje dźwiękowe. Więcej szczegółów na temat wszystkich dźwięków w tej symulacji można znaleźć w opublikowanej dokumentacji Sound Design Documentation.

Spostrzeżenia na temat korzystania z aplikacji przez uczniów

• Uczniowie bez doświadczenia w analizie Fouriera lub mechanice kwantowej mogą się wiele nauczyć z pierwszych dwóch ekranów. Trzeci ekran zwykle wymaga więcej wskazówek.
• Uczniowie często mylą funkcje przestrzeni i czasu i używają terminów "długość fali" i "okres" zamiennie. Możliwość przełączania się między tymi dwoma terminami (lub stosowania obu z nich) oraz korzystanie z narzędzi długości fali i okresu pomaga im lepiej je rozróżniać.
• Uczniowie często myślą, że długość fali i okres są właściwościami konkretnego miejsca na wykresie. Przesuwanie narzędzi długości fali i okresu może pomóc im zobaczyć, że tak nie jest.

Uproszczenia modelu

• Na ekranie Forma dyskretna wyrażenia z szeregu Fouriera nazywamy "harmonicznymi", ponieważ każda z nich ma częstotliwość będącą całkowitą wielokrotnością częstotliwości podstawowej. Jednak na ekranie Paczka falowa wyrażenia wyświetlane na wykresie Składowe nie są harmonicznymi, więc używamy bardziej ogólnego terminu "składowa".
• Pole wyboru Nieskończony szereg harmonicznych na ekranie Forma dyskretna wyświetla przebieg wynikający z nieskończonej liczby składowych harmonicznych. Jest ono aktywne tylko dla przebiegów trójkątnych, kwadratowych i piłokształtnych.
• Gra wymaga dokładnych odpowiedzi, aby można je było uznać za poprawne.
• Używamy konwencji dotyczącej liczby falowej k, zwykle stosowanej w fizyce (k = 2π/λ), a nie konwencji stosowanej w spektroskopii (k = 1/λ).
• Na ekranie Paczka falowa, σ_k i σ_x są odchyleniami standardowymi krzywych Gaussa odpowiednio w przestrzeni Fouriera i położenia. Podlegają one zasadzie nieoznaczoności σ_kσ_x=1. Używamy raczej σ_k niż Δk, ponieważ uczniowie interpretowali to jako "zmianę k". Łatwiej jest również wskazać szerokość na wykresach za pomocą odchylenia standardowego niż niepewności.
• Składowe na ekranie Paczka falowa to wyrazy w szeregu Fouriera. Pojawiają się one w ustalonych miejscach, a ich amplitudy zmieniają się wraz ze zmianą środka lub szerokości paczki falowej. Rozkład może okazać się asymetryczny, jeśli rozstaw między składowymi jest duży, odchylenie standardowe jest małe lub środek nie pokrywa się z rozstawem składowych.
• Zakresy suwaków na ekranie Paczka falowa zostały wybrane w celu uniknięcia niedostatecznego próbkowania, które występowało w wersji Java.
• Radiany są bezwymiarowe i pomijane w mianowniku dla σ_x i σ_t.
• Wszystkie osie y na ekranie Paczka falowa są skalowane automatycznie. Skala osi y dla wykresów Amplitudy i Składowe nie będzie jednak zgodna. Jeśli środek paczki falowej nie jest całkowitą wielokrotnością rozstawu składowych, maksymalna amplituda składowych będzie mniejsza niż szczytowa amplituda fali ciągłej.

Sugestie dotyczące wykorzystania

Wskazówki dotyczące wszystkich symulacji zawarte są w informacjach ogólnych.

Więcej porad dotyczących korzystania z symulacji z uczniami można znaleźć na stronach PhET w sekcji Wskazówki dotyczące korzystania z PhET.

Przykładowe polecenia

• Przewiduj, co stanie się z falą trójkątną, kwadratową lub piłokształtną, gdy liczba składowych harmonicznych zostanie zwiększona lub zmniejszona.
• Określ, który element wykresu Suma jest opisany przez każdy z symboli w równaniu.
• Opisz procedurę zastosowaną w celu dopasowania do różowego przebiegu fali.
• Porównaj i skontrastuj opis fal w przestrzeni i fal w czasie.
• Wyjaśnij zależność między σ_k i σ_x.

Zobacz wszystkie opublikowane na stronach PhET aktywności dla Fourier: Konstruowanie fal tutaj (dostęp do materiałów wymaga zalogowania).