Instrukcje dla nauczyciela do symulacji PhET - Pochodne i całki - wykresy
Symulacja Pochodne i całki - wykresy pozwala uczniom badać, sprawdzać i odkrywać powiązania między wykresami funkcji, jej całki, pierwszej pochodnej i drugiej pochodnej.
PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu Na licencji CC BY 4.0
W opracowaniu niniejszego poradnika wykorzystano materiały PhET: Strona źródłowa symulacji, Opis modelu oraz Teacher Tips (McGarry, kwiecień 2023)
W szablonie strony wykorzystano kod html/css: phydemo.app.
Szkoła średnia
Aplikacja Pochodne i całki - wykresy została zaprojektowana, aby pomóc uczniom w wizualizacji i zrozumieniu pojęć z zakresu rachunku różniczkowego, w szczególności dotyczących wykresów funkcji, pochodnych i całek. Główne funkcjonalności aplikacji obejmują:
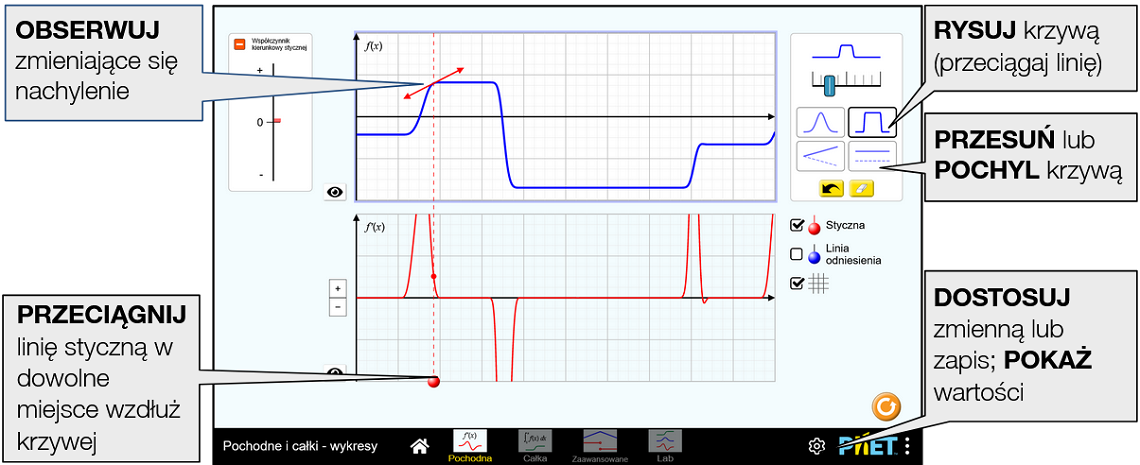
Na ekranie Pochodna uczniowie mogą manipulować wykresem funkcji i przeglądać wykres jej pochodnej.
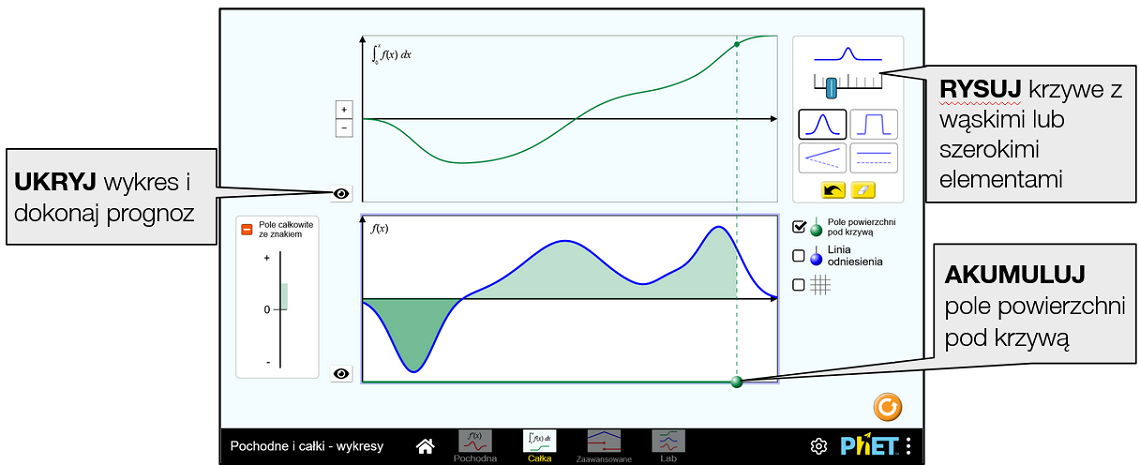
Na ekranie Całka uczniowie mogą wchodzić w interakcje z funkcją i oglądać wykres jej całki.
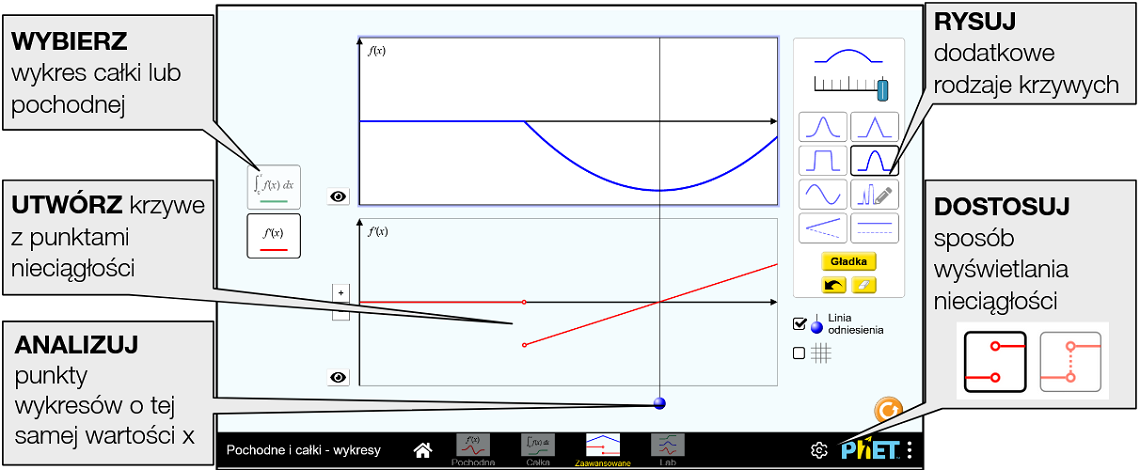
Na ekranie Zaawansowane uczniowie mają dostęp do dodatkowych narzędzi do rysowania, w tym do krzywych, które powodują nieciągłość pochodnej.
Na ekranie Lab uczniowie mogą wyświetlać do trzech wykresów jednocześnie i korzystać ze wszystkich zaawansowanych narzędzi do rysowania.
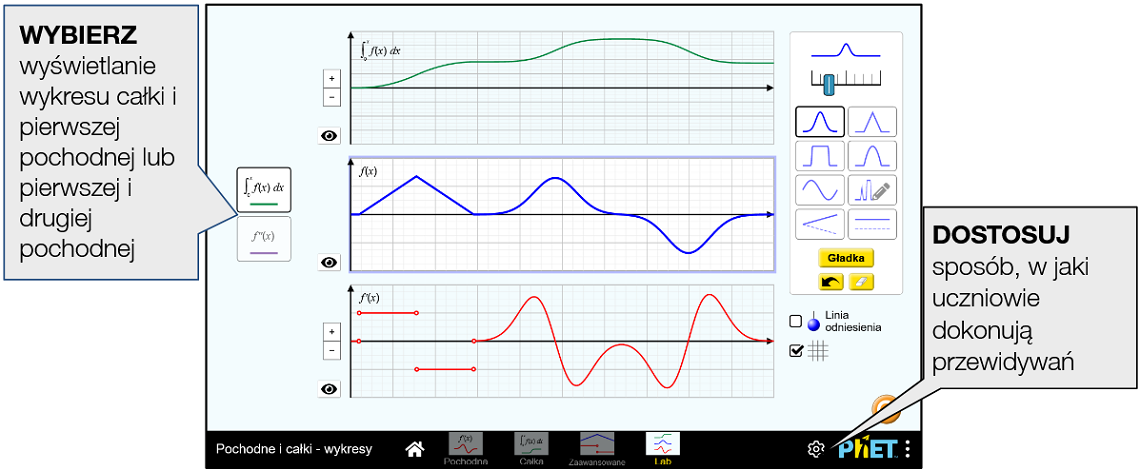
Panel sterowania po prawej stronie zawiera narzędzia do rysowania i opcje przeglądania. Pierwszą kontrolką jest suwak kontrolujący szerokość krzywej. Przesunięcie w prawo powoduje poszerzenie krzywej, a przesunięcie w lewo zawężenie.
Przyciski opcji pozwalają użytkownikowi wybierać spośród różnych funkcji trybu manipulacji krzywą (więcej szczegółów na temat każdego trybu znajduje się poniżej). Gdy użytkownik wybierze część wykresu, zaktualizuje się odpowiedni fragment.
Pod pionowymi przyciskami opcji pojawiają się przyciski Cofnij i Gumka. Przycisk Cofnij, reprezentowany przez strzałkę wstecz, usuwa ostatnią zmianę dokonaną w wykresie funkcji. Przycisk Gumka resetuje funkcję f(x) do stanu początkowego (który zazwyczaj wynosi y=0).
Poniżej panelu sterowania znajduje się pole wyboru Linia odniesienia, oznaczone pionową linią. Po zaznaczeniu na wykresach pojawi się linia odniesienia. Linia odniesienia obejmuje wszystkie wykresy, a położenie x linii odniesienia jest kontrolowane przez użytkownika.
Przyciski powiększenia są dostępne po lewej stronie wykresów pochodnej i całki. Umożliwiają one użytkownikowi zwiększenie lub zmniejszenie skali osi y.
Ponadto pod panelem sterowania znajduje się pole wyboru Siatka. Po zaznaczeniu każdy wykres będzie zawierał niezależne wewnętrzne linie siatki. Linie siatki będą skalowane odpowiednio do poziomu powiększenia.
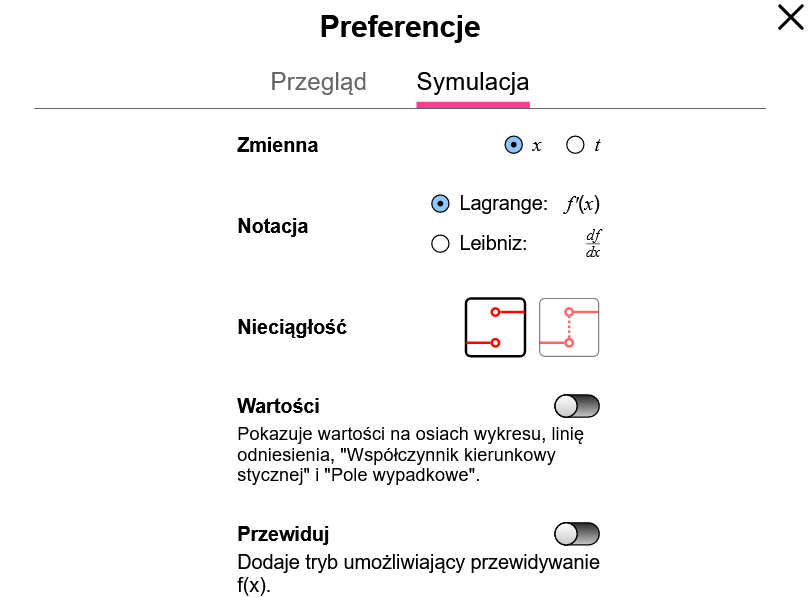
Ustawienia można znaleźć w zakładce okna dialogowego Preferencje
. Dostępnych jest pięć ustawień:
W górnej części ekranu pochodnej znajduje się funkcja f(x). Pod funkcją f(x) generowany jest wykres pochodnej. Widoczność krzywej na każdym wykresie jest kontrolowana za pomocą przycisku przełączania (oko 
) po lewej stronie każdego wykresu.
Do wyznaczenia pochodnej stosowana jest metoda różnic skończonych. Aby zilustrować punkty nieróżniczkowalne w f(x), otwarte kółka pojawiają się w punktach nieróżniczkowalnych na wykresie pochodnej.
Pole wyboru Styczna poniżej panelu sterowania uruchamia widoczność trzech elementów: (1) kontrolowanego przez użytkownika suwaka-kółka na dole wykresów, (2) strzałki stycznej na wyjściowym wykresie f(x) oraz (3) chowanej ramki z wykresem słupkowym wskazującym Współczynnik kierunkowy stycznej. Użytkownik może przesuwać w poziomie suwak-kółko, aby zmienić położenie x punktu styczności.
W górnej części ekranu Całka znajduje się całka oznaczona funkcji f(x). Pod tym wykresem wyświetlana jest funkcja kontrolowana przez użytkownika f(x). Całkę oznaczoną oblicza się numerycznie za pomocą trapezowej sumy Riemanna.
Pole wyboru Pole powierzchni pod krzywą poniżej panelu sterowania uruchamia widoczność trzech elementów: (1) kontrolowanego przez użytkownika suwaka-kółka na dole wykresów, (2) zaznaczenie pola pod krzywą na wyjściowym wykresie f(x) oraz (3) chowanej ramki z wykresem słupkowym Pole całkowite ze znakiem wskazującym wartość pola powierzchni pod krzywą. Użytkownik może przesuwać w poziomie suwak-kółko, aby zmienić górną granicę całkowania.
Ekran Zaawansowane zawiera dwie główne funkcje, których nie ma na poprzednich ekranach. Po lewej stronie wykresów dodano zestaw dwóch prostokątnych przycisków. Umożliwiają one przełączanie między wykresami pochodnej i całki.
Do panelu sterowania dodano przycisk Gładka, który wygładza oryginalną funkcję f(x), obliczając jej lokalną średnią. Przycisk Gładka można nacisnąć wiele razy, aby jeszcze bardziej wygładzić funkcję.
Wybór funkcji został rozszerzony o funkcje trójkątne, paraboliczne, sinusoidalne i o dowolnym kształcie.
Ekran Lab zawiera wszystkie funkcje z ekranu Zaawansowane i dodaje trzeci wykres na ekranie.
Użytkownik może manipulować wyjściową funkcją za pomocą zestawu trybów manipulacji krzywą. W tej symulacji dostępnych jest osiem trybów:
jest bardzo przydatny do zmniejszenia tego szumu i można go kliknąć wiele razy, aby wygładzić ręcznie narysowaną krzywą.
) jest narzędziem umożliwiającym nauczycielom lub uczniom zbudowanie funkcji, która tworzy określone wykresy pochodnej i całki, ukrywa oryginalną funkcję, ale wchodzi w interakcję z krzywą przewidywania, gdy uczniowie zastanawiają się nad właściwościami f(x), które dałyby dane wykresy pochodnej i całki.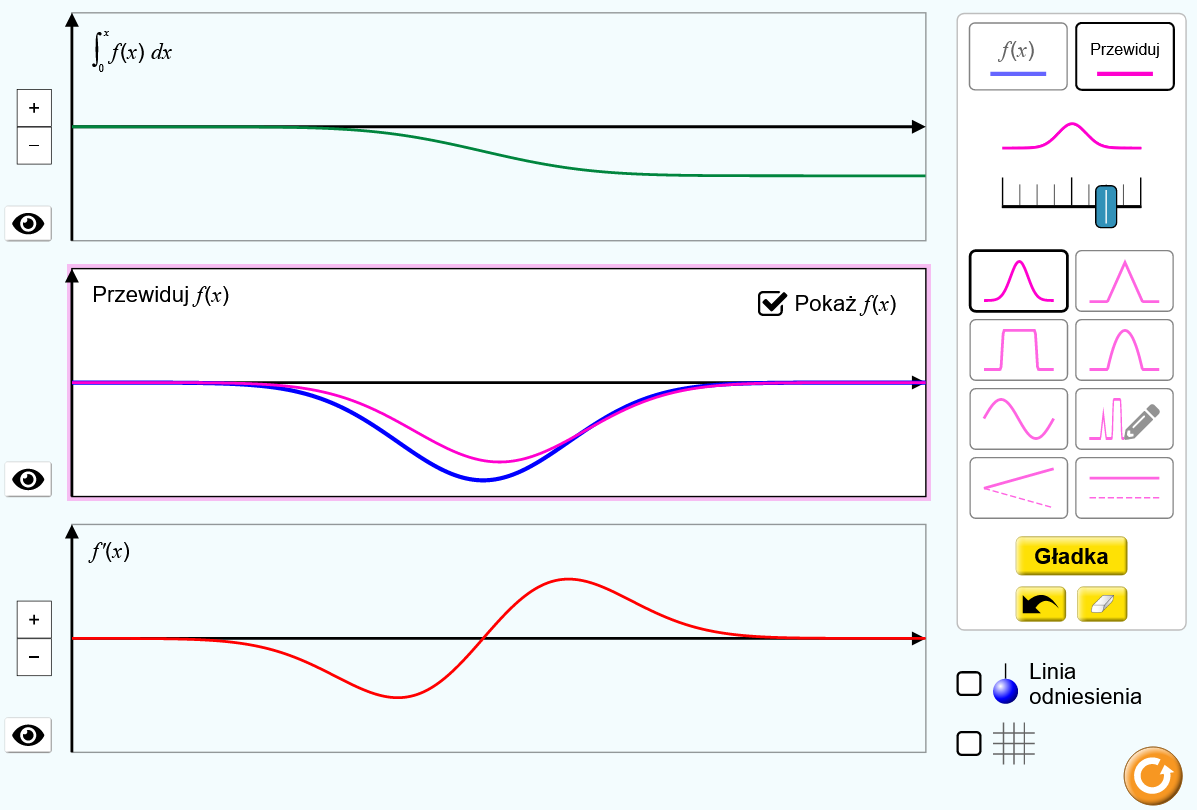
Poniższe parametry query umożliwiają dostosowanie symulacji i można je dodać, dołączając znak '?' do adresu URL symulacji i oddzielając każdy parametr query znakiem '&'. Ogólny wzorzec adresu URL to: …html?queryParameter1&queryParameter2&queryParameter3
Na przykład, jeśli w aplikacji Pochodne i całki - wykresy chcesz zmienić kolejność ekranów (screens=2,1), z domyślnie otwartym drugim ekranem (initialScreen=2), użyj: https://www.edukator.pl/simulations/calculus-grapher_all.html?screens=2,1&initialScreen=2
Aby uruchomić to w języku polskim (locale=pl), adres URL będzie wyglądał następująco: https://www.edukator.pl/simulations/calculus-grapher_all.html?locale=pl&screens=1,2&initialScreen=2
Wskazuje, że dostęp do tego dostosowania można uzyskać też z menu Preferencje w symulacji.
| Parametr query i opis | Przykłady |
| screens - określa, które ekrany są włączone do symulacji i jaka jest ich kolejność. Każdy ekran powinien być oddzielony przecinkiem. Więcej informacji można znaleźć w Centrum pomocy. | screens=2,1 screens=3 |
| functionVariable - określa, czy x czy t jest używaną zmienną. | functionVariable=t |
| derivativeNotation - określa sposób zapisu pochodnej używany w całej symulacji. Możliwe wartości: lagrange lub leibniz. | derivativeNotation=leibniz |
| connectDiscontinuities - określa, czy nieciągłości mają być połączone linią przerywaną (dashedLine) czy nie (noLine). | connectDiscontinuities=dashedLine |
| valuesVisible - pokazuje wartości liczbowe tam, gdzie mogą pojawić się w symulacji: osie (etykiety zaznaczenia), współczynnik kierunkowy stycznej, pole powierzchni wypadkowej ze znakiem. | valuesVisible=true |
| predict - określa, czy tryb Przewiduj jest widoczny. | predict=true |
| initialScreen - otwiera kartę SIM bezpośrednio na określonym ekranie, z pominięciem ekranu głównego. | initialScreen=1 initialScreen=2 |
| locale - określa język symulacji przy użyciu kodów ISO 639-1. Dostępne wersje językowe można znaleźć na stronie symulacji w zakładce Tłumaczenia. Uwaga: działa to tylko wtedy, gdy adres URL symulacji kończy się na “_all.html”. | locale=pl (polski) locale=fr (francuski) |
| allowLinks - jeśli false, wyłącza linki, które prowadzą uczniów do zewnętrznego adresu URL. Domyślnie jest true. | allowLinks=false |
| supportsPanAndZoom - gdy true, umożliwia przesuwanie i powiększanie symulacji za pomocą pinch-to-zoom lub elementów sterujących zoomem przeglądarki. | supportsPanAndZoom=false |
Po kliknięciu logo PhET (na dole po prawej) pojawia się okno zawierające informacje dotyczące symulacji. Możemy tu zmienić sposób jej wyświetlania.
Klikając Pełny ekran przechodzimy do trybu pełnoekranowego (powrót - klawisz escape).
Dostępne są również wersje symulacji niewymagające połączenia z internetem.
Aplikacja PhET Desktop zawiera wszystkie symulacje HTML5 i Java, w tym ich tłumaczenia, do użytku offline w systemach Windows i macOS (dostępne po zalogowaniu tu). Symulacje HTML5 nie wymagają dodatkowego oprogramowania, natomiast do uruchamiania dowolnych symulacji Java w aplikacji komputerowej jest wymagany Java SE Development Kit 8.
Za symboliczną opłatą możemy pobrać w postaci jednej aplikacji wszystkie materiały PhET, które zostały opublikowane w html5. Telefony, tablety i Chromebooki (z systemem Android): Google Play. iPhone'y i iPady (aplikacja na iOS): App Store
Darmową wersję desktopową tej aplikacji pobierzemy bezpośrednio klikając tu - wersja _pl zawiera polską (domyślną) i angielską wersję językową i tu - wersja _all zawiera angielską (domyślną) i wszystkie inne dostępne wersje językowe lub ze strony PhET (klikając przycisk ze strzałką przy wybranej wersji językowej):
Przybliżamy krzywe, generując zestaw dyskretnych punktów o stałych współrzędnych x. Każda krzywa zawiera 1251 punktów. Każdy punkt na krzywej ma określone metadane typu punktu, takie jak gładki, szpic lub nieciągłość. Funkcja ma nieciągłość skokową, jeśli lewa i prawa granica funkcji nie są równe. W takich przypadkach punkty po obu stronach skoku są oznaczane jako nieciągłe. Podobnie, punkty są oznaczane jako szpic, jeśli nachylenie krzywej nagle się zmienia. Wykorzystujemy typ punktu, aby określić, które punkty powinny być połączone, aby uzyskać wygląd gładkiej krzywej, a które punkty nie powinny być połączone, ale pojawiają się jako okręgi ( aby reprezentować nieciągłości). Manipulacje krzywymi są obsługiwane przez zestaw funkcji, które aktualizują punkty krzywej na podstawie danych wprowadzonych przez użytkownika. Typ punktu jest oceniany na podstawie typu trybu krzywej, która jest modyfikowana.
Matematycznie, krzywa całkowa jest obliczana jako lewa suma Riemanna na podstawie punktów na krzywej f(x). Metadane typu punktu krzywej całkowej są oparte na metadanych punktu krzywej f(x), przy czym punktom szpicowym są przypisywane punkty gładkie, a punktom nieciągłym - punkty szpicowe.
Funkcje pochodne, takie jak pierwsza i druga pochodna, są obliczane przy użyciu metody różnic skończonych opartej na sąsiednich punktach. Na przykład pochodna funkcji f(x) jest przybliżana przez obliczenie współczynnika kierunkowego pomiędzy sąsiednimi punktami. Szczególną uwagę zwraca się na punkty zidentyfikowane jako szpice i nieciągłości, w których linia sieczna jest obliczana z odpowiednio wybranym punktem sąsiednim. Metadane typu punktu pochodnej są dziedziczone z krzywej f(x), z wyjątkiem tego, że punkty szpicowe są klasyfikowane jako nieciągłości dla pochodnych.
Druga pochodna jest obliczana na podstawie centralnego ilorazu różnicowego drugiego rzędu funkcji f(x). Metadane typu punktu drugiej pochodnej są dziedziczone z krzywej f(x), z wyjątkiem tego, że punktom szpicowym są przypisywane nieciągłości dla drugiej pochodnej. Druga pochodna punktów nieciągłych jest aproksymowana jako równa jej gładkiemu punktowi sąsiedniemu.
Funkcja cofania jest realizowana poprzez zapisanie stosu poprzednich stanów krzywej. Za każdym razem, gdy użytkownik wykonuje akcję, która modyfikuje krzywą, taką jak wygładzanie lub manipulacja krzywą, bieżący stan krzywej jest zapisywany na końcu akcji i umieszczany w stosie. Gdy użytkownik wywoła funkcję cofania, najnowszy stan jest usuwany ze stosu i używany do przywrócenia krzywej. Zapisujemy do 20 ostatnich stanów krzywej.
Wskazówki dotyczące wszystkich symulacji zawarte są w informacjach ogólnych.
Więcej porad dotyczących korzystania z symulacji z uczniami można znaleźć na stronach PhET w sekcji Wskazówki dotyczące korzystania z PhET.
Zobacz wszystkie opublikowane na stronach PhET aktywności dla Pochodne i całki - wykresy tutaj (dostęp do materiałów wymaga zalogowania).