Dopasowanie krzywej

Zagadnienia

• Wielomiany
• Analiza błędów
• Dane

Opis

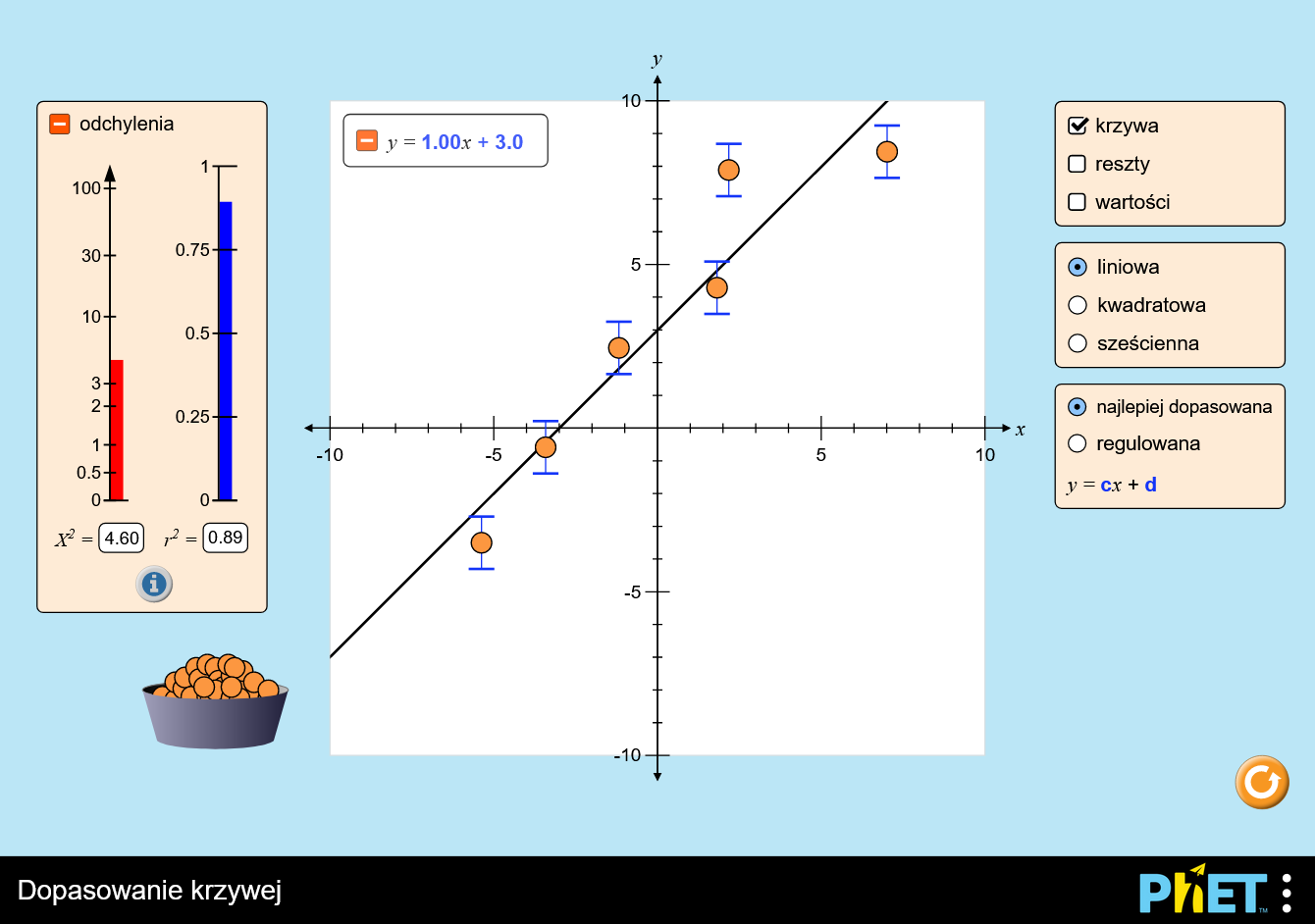
Symulacja Dopasowanie krzywej demonstruje podejście dopasowania krzywej metodą najmniejszych kwadratów do krzywych wielomianowych. Przeciągając punkty danych z kubełka na wykres, użytkownik jest proszony o znalezienie krzywej najlepszego dopasowania dla punktów danych na wykresie. Do każdego punktu danych przypisany jest błąd (niepewność). Użytkownik może manipulować błędem każdego punktu danych, zmieniając położenie słupków błędów. Symulacja pozwala uczniom zbadać, w jaki sposób liczba punktów danych i niepewność ich dotycząca może wpływać na chi kwadrat i r kwadrat.

PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu Na licencji CC BY 4.0

W opracowaniu niniejszego poradnika wykorzystano materiały PhET: Strona źródłowa symulacji, Teacher Tips (McGarry, sierpień 2023)

W szablonie strony wykorzystano kod html/css: phydemo.app.

Poziom

Szkoła średnia

Przykładowe cele nauczania

• Wyjaśnij, w jaki sposób zakres i niepewność oraz liczba punktów danych wpływają na współczynnik korelacji i chi kwadrat
• Opisz, w jaki sposób można wykorzystać współczynnik korelacji i chi-kwadrat do wskazania, jak dobrze krzywa opisuje zależność między danymi
• Zastosuj zrozumienie dopasowania krzywej do projektowania eksperymentów

Przykładowe materiały teoretyczne

• Jak dopasować prostą do wyników pomiarów? (ZPE)
• W jakim celu dopasowuje się prostą do wyników pomiarów i jakie informacje można w ten sposób uzyskać? (ZPE)
• Na ile dokładnie można dopasować prostą do wyników pomiarów? (ZPE)
• Dane i modelowanie (Khan Academy)
• Statystyka i prawdopodobieństwo (Khan Academy)

Sterowanie symulacją

Ekran symulacji

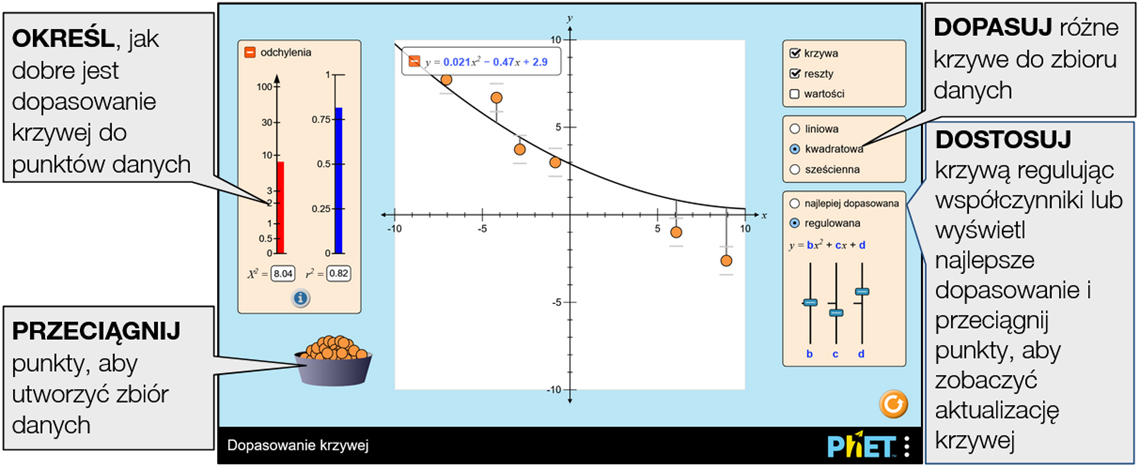
Przeciągnij myszką punkty danych i ich słupki błędów i od razu obejrzyj aktualizację krzywej wielomianowej, która jest najlepiej dopasowana. Wybierz typ dopasowania: funkcja liniowa, kwadratowa lub trzeciego stopnia. Zredukowane chi-kwadrat pokazuje, kiedy dopasowanie jest dobre. Możesz też spróbować znaleźć najlepsze dopasowanie, ręcznie dostosowując parametry.

Opcje dostosowywania

Poniższe parametry query umożliwiają dostosowanie symulacji i można je dodać, dołączając znak '?' do adresu URL symulacji i oddzielając każdy parametr query znakiem '&'. Ogólny wzorzec adresu URL to: …html?queryParameter1&queryParameter2&queryParameter3

Na przykład, jeśli symulację Dopasowanie krzywej chcesz uruchomić w języku hiszpańskim (screens=1,2), z wyłączonymi linkami zewnętrznymi (initialScreen=2), użyj: https://www.edukator.pl/tik_edukator/curve-fitting_all.html?locale=es&allowLinks=false

Parametr query i opis	Przykładowe linki
locale - określa język symulacji przy użyciu kodów ISO 639-1. Dostępne wersje językowe można znaleźć na stronie symulacji w zakładce Tłumaczenia. Uwaga: działa to tylko wtedy, gdy adres URL symulacji kończy się na “_all.html”.	locale=pl (polski) locale=fr (francuski)
allowLinks - jeśli false, wyłącza linki, które prowadzą uczniów do zewnętrznego adresu URL. Domyślnie jest true.	allowLinks=false

Ułatwienia dostępu

Tryb pełnoekranowy

Po kliknięciu logo PhET (na dole po prawej) pojawia się okno zawierające informacje dotyczące symulacji. Możemy tu zmienić sposób jej wyświetlania.

Klikając Pełny ekran przechodzimy do trybu pełnoekranowego (powrót - klawisz escape).

Wersje offline, niewymagające połączenia z internetem

Dostępne są również wersje symulacji niewymagające połączenia z internetem.

Aplikacja PhET Desktop zawiera wszystkie symulacje HTML5 i Java, w tym ich tłumaczenia, do użytku offline w systemach Windows i macOS (dostępne po zalogowaniu tu). Symulacje HTML5 nie wymagają dodatkowego oprogramowania, natomiast do uruchamiania dowolnych symulacji Java w aplikacji komputerowej jest wymagany Java SE Development Kit 8.

Za symboliczną opłatą możemy pobrać w postaci jednej aplikacji wszystkie materiały PhET, które zostały opublikowane w html5. Telefony, tablety i Chromebooki (z systemem Android): Google Play. iPhone'y i iPady (aplikacja na iOS): App Store

Darmową wersję desktopową tej aplikacji pobierzemy bezpośrednio klikając tu - wersja _pl zawiera polską (domyślną) i angielską wersję językową i tu - wersja _all zawiera angielską (domyślną) i wszystkie inne dostępne wersje językowe lub ze strony PhET (klikając przycisk ze strzałką przy wybranej wersji językowej):

Spostrzeżenia na temat korzystania z aplikacji przez uczniów

• Uczniowie mogą mieć doświadczenie ze współczynnikiem korelacji \(r^{2}\) korzystając z kalkulatorów graficznych i programu Excel (lub innego arkusza kalkulacyjnego). Mogą nie zaobserwować reszt, jeśli wszystkie ich punkty danych znajdują się na krzywej. Upewnij się, że podczas korzystania z symulacji wykorzystano wiele punktów z pewnymi odchyleniami.

Uproszczenia / założenia modelu

• Symulacja umożliwia dopasowanie 3 typów krzywych wielomianowych: liniowej, kwadratowej i stopnia trzeciego. Dopasowanie można wykonać ręcznie (regulowana), manipulując zestawem suwaków lub określić automatycznie (najlepiej dopasowana).
• Wartości \(\chi ^{2}\) i \(r^{2}\) są określane dla krzywej w odniesieniu do punktów danych i wyświetlane za pomocą wskaźnika słupkowego. Współczynniki najlepszego dopasowania są obliczane przy użyciu standardowej procedury ważonej regresji najmniejszych kwadratów, w której można znaleźć najbardziej odpowiednie współczynniki wielomianowe, które minimalizują wartość \(\chi ^{2}\).
• Wartość \(\chi ^{2}\) jest szacowana jako suma kwadratów odchylenia między wartością obserwowanego punktu a odpowiadającą mu wartością krzywej. Każdy punkt danych w sumie jest ważony czynnikiem, który jest odwrotnie proporcjonalny do kwadratu jego niepewności. Wartość \(r^{2}\) jest obliczana jako jeden minus stosunek ważonej wyjaśnionej sumy kwadratów do ważonej resztowej sumy kwadratów.
• Wzory do obliczania odchyleń wykorzystują zredukowaną statystykę \(\chi ^{2}\).
• \(\Delta_{y}\) i \(\sigma\) reprezentują tę samą ideę, ale konwencje wyświetlania graficznego i równań nie są takie same. Termin słupek błędu jest powszechnie używany w odniesieniu do niepewności punktu danych na wykresie. Technicznie rzecz biorąc, połowa wysokości słupka błędu jest równa jednemu odchyleniu standardowemu. Symbol \(\sigma_{i}\) jest konwencjonalnie używany w odniesieniu do niepewności punktu danych \((x_{i},y_{i})\) w równaniach.
• Więcej informacji dotyczących założeń modelu można uzyskać tu (en)

Sugestie dotyczące wykorzystania

Wskazówki dotyczące wszystkich symulacji zawarte są w informacjach ogólnych.

Więcej porad dotyczących korzystania z symulacji z uczniami można znaleźć na stronach PhET w sekcji Wskazówki dotyczące korzystania z PhET.

Ta symulacja może być wykorzystana jako wprowadzenie do statystyki bez konieczności uczenia się, jak oblicza się \(\chi^{2}\).

Przykładowe polecenia

• Zbuduj zestaw danych i zdecyduj, która krzywa najlepiej pasuje do Twoich danych. Jak można się o tym przekonać?
• Jaki wpływ ma zmiana słupków niepewności na \(\chi^{2}\) i \(r^{2}\)?
• Dla każdego z typów dopasowania krzywej, jaka jest minimalna liczba punktów, aby uzyskać zieloną strefę dla \(\chi^{2}\) i dobrą korelację?

Zobacz wszystkie opublikowane na stronach PhET aktywności dla Dopasowanie krzywej tutaj (dostęp do materiałów wymaga zalogowania).