Interaktywny plik html wygenerowany przez Sketchometry, dotyczący wykresu funkcji liniowej.
Zagadnienia
- Funkcja liniowa
- Współczynnik kierunkowy
- Wyraz wolny
Opis
Materiały dotyczące tworzenia wykresu funkcji liniowej za pomocą narzędzia Sketchometry (Center for Mobile Learning with Digital Technology, University of Bayreuth).
Koncepcja modułów nauczania sketchometry - podzielonych na fazy konstruowania, badania, odręcznej dokumentacji, dyskusji i prezentacji - ma na celu promowanie samodzielnej pracy i uczenia się opartego na dociekaniu. Uczniowie otrzymują papierowy arkusz roboczy z zadaniami i poleceniami dostosowanymi do ich poziomu i używają tabletu lub smartfona jako elektronicznego szkicownika. Swoje obserwacje, odkrycia i założenia zapisują odręcznie w arkuszu wyników lub w zeszycie. Więcej informacji tu (en).
Poniższe materiały mają za zadanie jedynie ułatwić nauczycielowi przygotowanie zróżnicowanych scenariuszy zajęć, zgodnych z tą koncepcją, dostosowanych do poziomu klasy czy indywidualnego ucznia lub ułatwić wykorzystanie gotowych kostrukcji podczas wykładu i nie powinny być traktowane jako instrukcja dla ucznia.
W opracowaniu niniejszego poradnika wykorzystano materiały zawarte na stronie źródłowej sketchometry.
W szablonie strony wykorzystano kod html/css: phydemo.app.
Poziom
Szkoła podstawowa, szkoła średnia
Wymagania wstępne i przykładowe cele nauczania
- Uczniowie znają równania liniowe postaci 𝑓(𝑥) = a ∙ 𝑥 + b.
- Uczniowie eksperymentalnie badają wpływ i znaczenie geometryczne parametrów a i b.
- Uczą się pojęć: punkt przecięcia wykresu z osią Y, nachylenie (tangens kąta nachylenia).
Przykładowe materiały teoretyczne
- Definicja funkcji liniowej (ZPE)
- Definicja funkcji liniowej (ZPE)
- Równanie liniowe (ZPE)
- Współczynnik kierunkowy funkcji liniowej (ZPE)
Uczniowie powinni wiedzieć
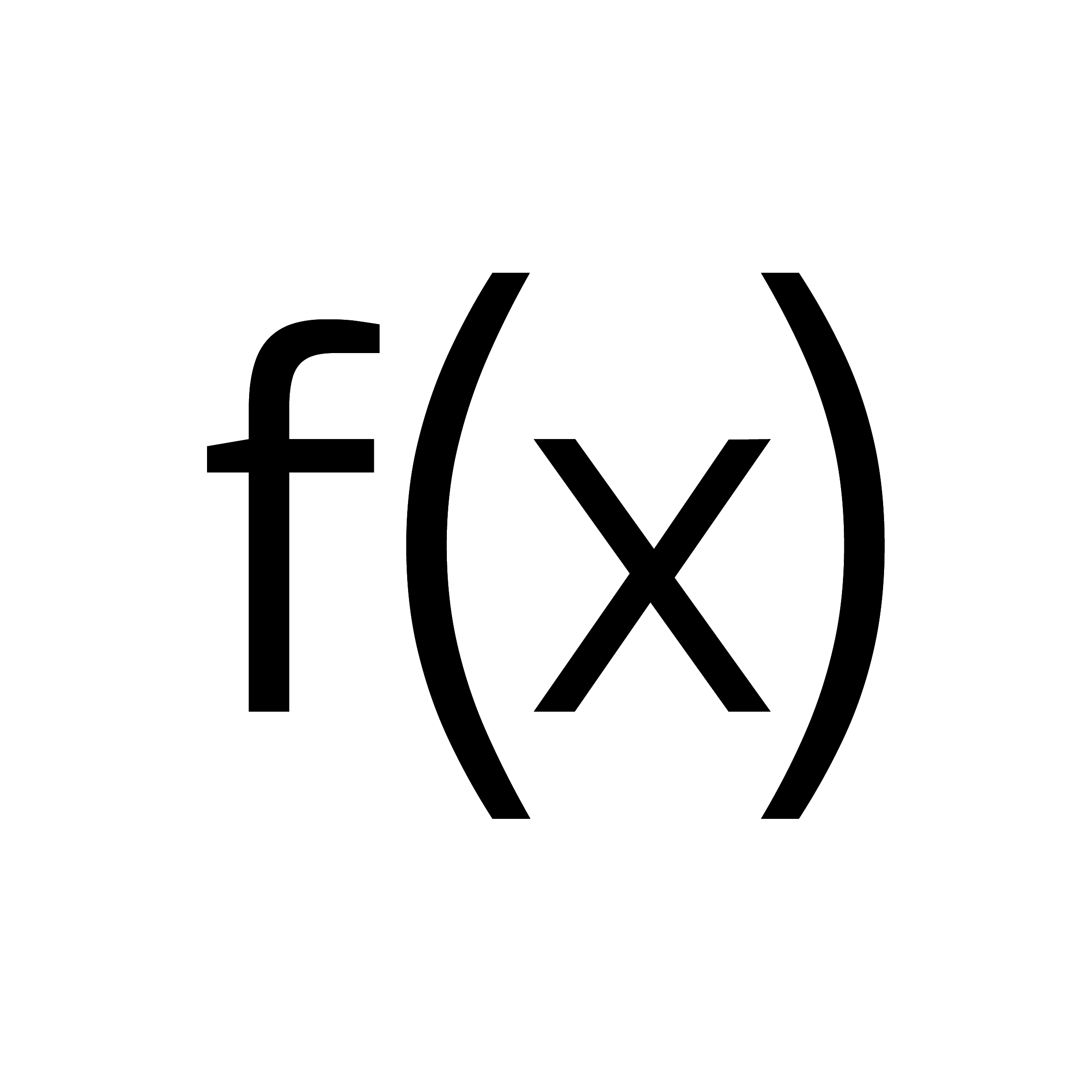


Arkusz roboczy
Konstrukcja
- Wyświetl siatkę i układ współrzędnych.
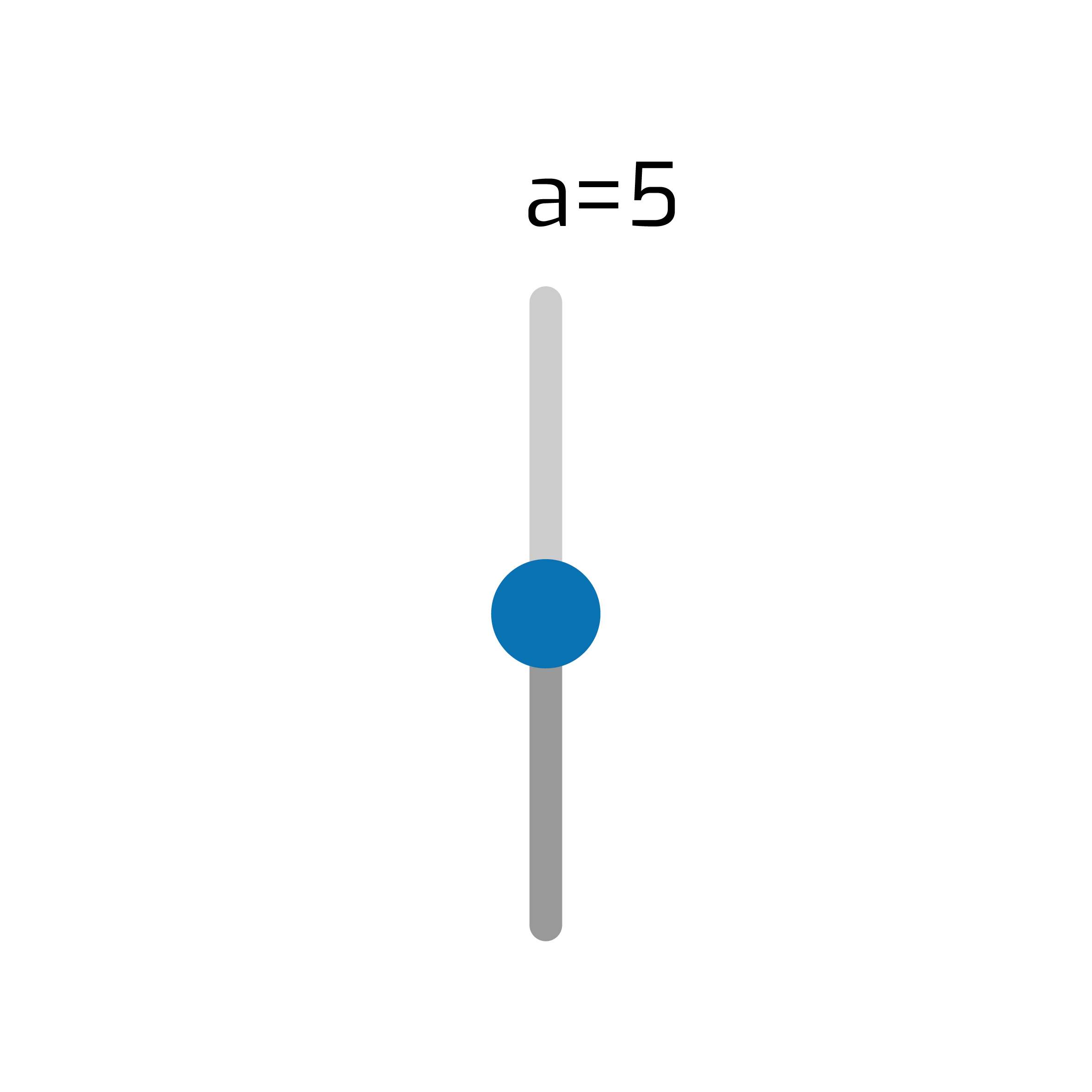
- W sekcji Funkcje wybierz Suwak, ustal zakres od -5 do 5, nadaj mu nazwę a i umieść go w prawym górnym rogu tablicy.
- Na prawo od niego umieść kolejny Suwak b, również o zakresie od −5 do 5.
- W obszarze Funkcje wybierz opcję f(x) Wykres funkcji i wprowadź wzór funkcji 𝑓(𝑥) = a ∙ 𝑥 + b. Dane wejściowe sketchometry: a*x+b
- Wybierz w obszarze Zmierz na pasku narzędzi Tekst. Następnie wpisz 𝑓(𝑥) = a ∙ 𝑥 + b i umieść tekst obok wykresu. Dane wejściowe sketchometry: $f(x)=m*x+t$
- Zaznacz punkty A i B przecięcia wykresu funkcji z osiami układu współrzędnych.
- Uaktywnij Zmierz na pasku narzędzi i kliknij punkty A i B, żeby podać ich współrzędne.
Badanie
- Przesuń suwak b i obserwuj wykres. Co zauważasz? Zanotuj swoje obserwacje.
- Przesuń suwak a i obserwuj wykres. Co zauważasz? Ponownie zrób notatki. Opisz różnicę w działaniu suwaka b.
- Wybierz wartość −2 dla b. Jaką wartość musi mieć a, aby wykres przecinał oś 𝑥 dokładnie w punkcie o odciętej 𝑥 = 4? Zapisz wynik za pomocą szkicu.
- Jakie jest geometryczne znaczenie parametrów a i b?
Wskazówka: Umieść punkt (slizgający się) na wykresie i stwórz trójkąt nachylenia. Przesuń trójkąt wzdłuż wykresu. Zapisz swoje obserwacje (ze szkicami).
- O czym decyduje znak a? Zapisz swoje odkrycie.
Dodatkowe informacje
Wskazówki dotyczące wszystkich symulacji zawarte są w Informacje ogólne, a poradnik dotyczący korzystania ze Sketchometry w Instrukcje - linki na górze strony.

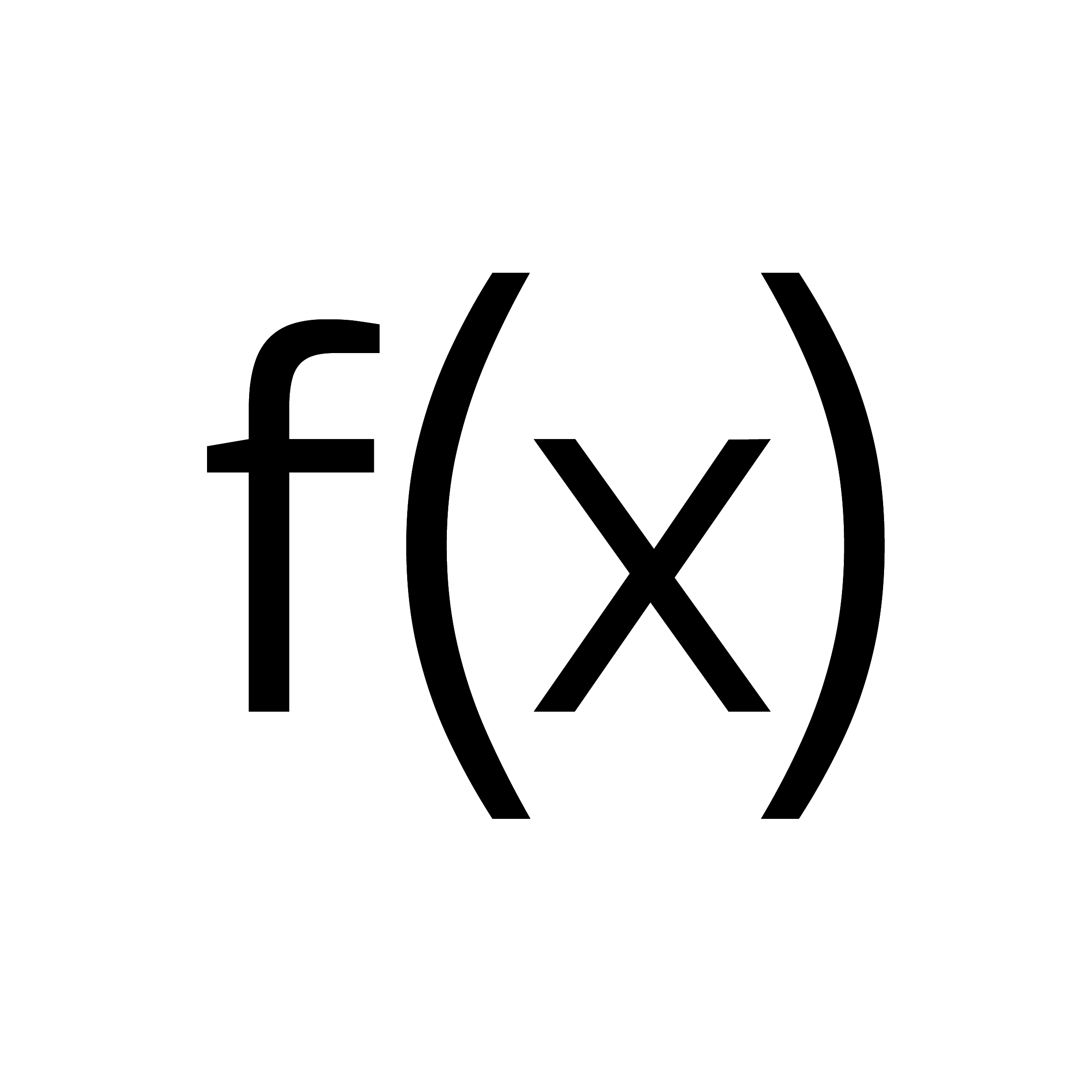


 Tablica →
Tablica →  , Właściwości →
, Właściwości →  Tablica →
Tablica →  )
)