Funkcje trygonometryczne

Zagadnienia

• Trygonometria
• Okrąg jednostkowy
• Sinusy
• Cosinusy
• Styczne

Opis

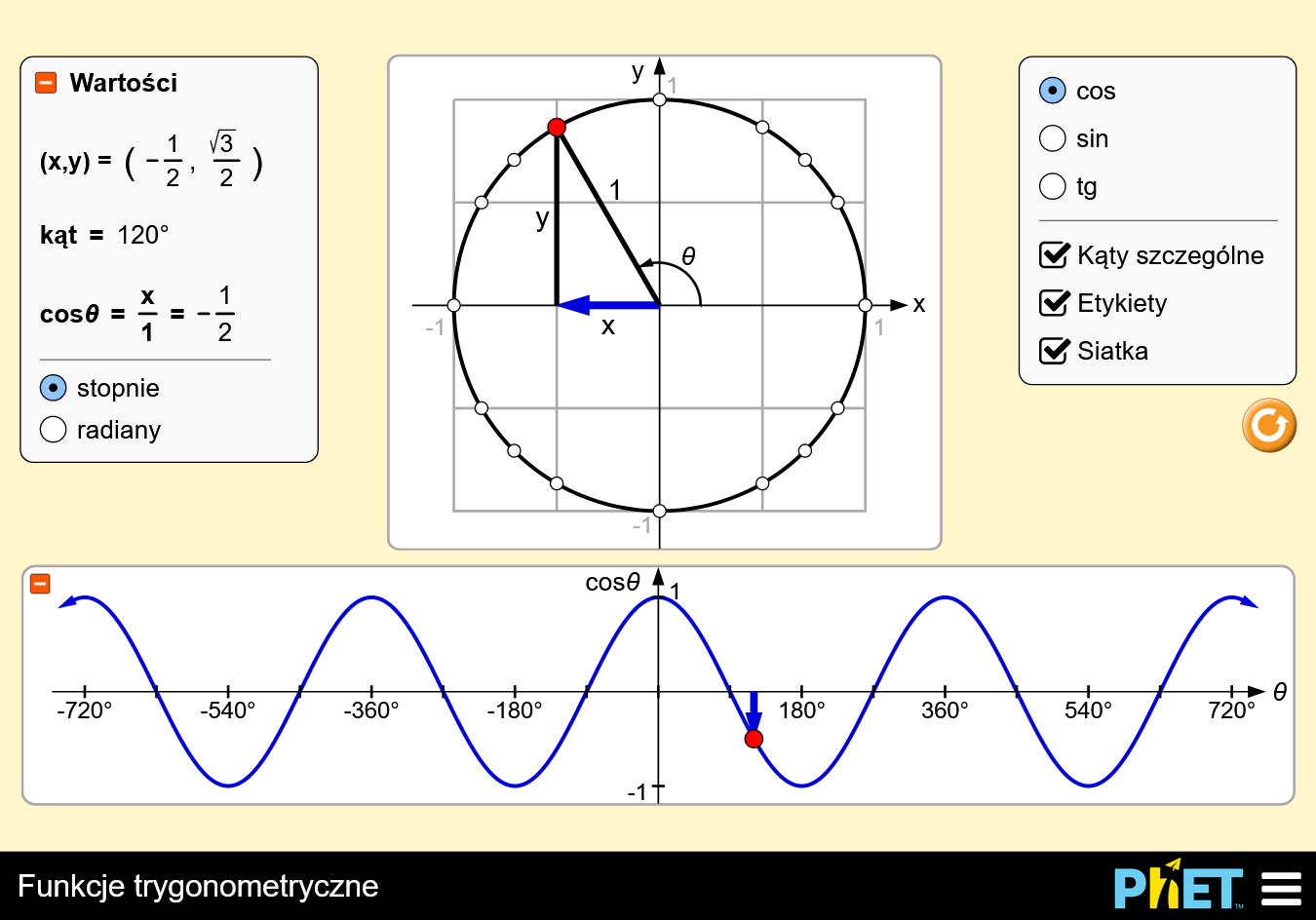
Interaktywna aplikacja umożliwia uczniom elastyczne przechodzenie między wieloma reprezentacjami funkcji trygonometrycznych, odkrywanie prawidłowości, szacowanie lub określanie dokładnych wartości funkcji trygonometrycznych oraz wnioskowanie o znaku (+, -, 0) funkcji trygonometrycznych dla dowolnego kąta bez użycia kalkulatora.

PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu Na licencji CC BY 4.0

W opracowaniu niniejszego poradnika wykorzystano materiały PhET: Strona źródłowa symulacji, Teacher Tips (Dalton, Hanson, McGarry, sierpień 2023)

W szablonie strony wykorzystano kod html/css: phydemo.app.

Poziom

Szkoła średnia

Przykładowe cele nauczania

• Zdefiniuj funkcje trygonometryczne dla kątów ujemnych i większych niż 90 stopni.
• Przechodź pomiędzy różnymi reprezentacjami funkcji trygonometrycznych: jako boki trójkąta prostokątnego wpisanego w okrąg jednostkowy, wykres funkcji w zależności od kąta oraz wartości liczbowe funkcji.
• Określ znak (+, -, 0) wartości funkcji trygonometrycznej dla dowolnego kąta bez użycia kalkulatora z wykorzystaniem koncepcji koła jednostkowego.
• Szacuj wartości funkcji trygonometrycznych dla dowolnego kąta bez kalkulatora, używając koncepcji koła jednostkowego.
• Określaj dokładne wartości funkcji trygonometrycznych dla kątów szczególnych, używając stopni lub radianów jako jednostek miary kąta.

Przykładowe materiały teoretyczne

• Funkcje trygonometryczne zmiennej rzeczywistej (ZPE)
• Koło trygonometryczne i zastosowania funkcji trygonometrycznych (Open AGH)
• Funkcje trygonometryczne (Khan Academy)

Sterowanie symulacją

Ekran symulacji

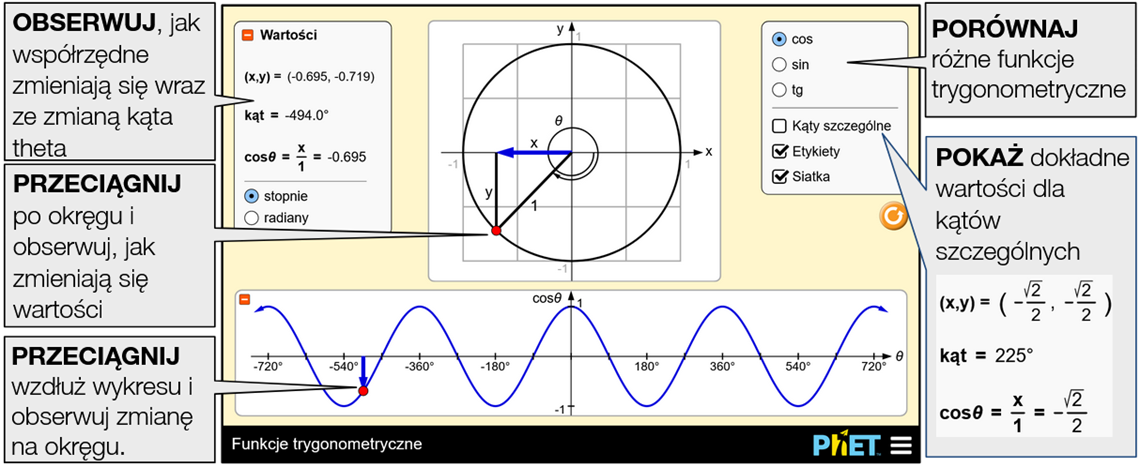
Definicje i wykresy funkcji trygonometrycznych. Okrąg jednostkowy. Wybierz się na wycieczkę po trygonometrii używając stopni lub radianów! Poszukaj prawidłowości w wartościach i na wykresie, gdy zmieniasz wartość kąta. Porównaj wykresy sinusa, cosinusa i tangensa.

Opcje dostosowywania

Poniższe parametry query umożliwiają dostosowanie symulacji i można je dodać, dołączając znak '?' do adresu URL symulacji i oddzielając każdy parametr query znakiem '&'. Ogólny wzorzec adresu URL to: …html?queryParameter1&queryParameter2&queryParameter3

Na przykład, jeśli aplikację Funkcje trygonometryczne chcesz uruchomić po hiszpańsku (locale=es), z wyłączonymi linkami zewnętrznymi (allowLinks=false), użyj: https://www.edukator.pl/tik_edukator/trig-tour_all.html?locale=es&allowLinks=false

Parametr query i opis	Przykładowe linki
locale - określa język symulacji przy użyciu kodów ISO 639-1. Dostępne wersje językowe można znaleźć na stronie symulacji w zakładce Tłumaczenia. Uwaga: działa to tylko wtedy, gdy adres URL symulacji kończy się na “_all.html”.	locale=pl (polski) locale=fr (francuski)
allowLinks - jeśli false, wyłącza linki, które prowadzą uczniów do zewnętrznego adresu URL. Domyślnie jest true.	allowLinks=false

Ułatwienia dostępu

Tryb pełnoekranowy

Po kliknięciu logo PhET (na dole po prawej) pojawia się okno zawierające informacje dotyczące symulacji. Możemy tu zmienić sposób jej wyświetlania.

Klikając Pełny ekran przechodzimy do trybu pełnoekranowego (powrót - klawisz escape).

Wersje offline, niewymagające połączenia z internetem

Dostępne są również wersje symulacji niewymagające połączenia z internetem.

Aplikacja PhET Desktop zawiera wszystkie symulacje HTML5 i Java, w tym ich tłumaczenia, do użytku offline w systemach Windows i macOS (dostępne po zalogowaniu tu). Symulacje HTML5 nie wymagają dodatkowego oprogramowania, natomiast do uruchamiania dowolnych symulacji Java w aplikacji komputerowej jest wymagany Java SE Development Kit 8.

Za symboliczną opłatą możemy pobrać w postaci jednej aplikacji wszystkie materiały PhET, które zostały opublikowane w html5. Telefony, tablety i Chromebooki (z systemem Android): Google Play. iPhone'y i iPady (aplikacja na iOS): App Store

Darmową wersję desktopową tej aplikacji pobierzemy bezpośrednio klikając tu - wersja _pl zawiera polską (domyślną) i angielską wersję językową i tu - wersja _all zawiera angielską (domyślną) i wszystkie inne dostępne wersje językowe lub ze strony PhET (klikając przycisk ze strzałką przy wybranej wersji językowej):

Spostrzeżenia na temat korzystania z aplikacji przez uczniów

• Jeśli uczniowie nie zostaną o to poproszeni, mogą nie zauważyć, że mogą przeciągać zarówno czerwoną kropkę wzdłuż okręgu jednostkowego, jak i czerwoną kropkę wzdłuż wykresu.
• Uczniowie mogą nadal przeciągać czerwoną kropkę wokół okręgu wiele razy, nawet gdy wykres wychodzi poza pole widzenia.

Uproszczenia / założenia modelu

• Jako separator dziesiętny używana jest kropka.
• Kąty mogą być zmieniane skokowo co pół stopnia.
• Kąty w radianach i wartości funkcji trygonometrycznych zaokrąglane są z dokładnością do 0,001, a gdy wybór kątów jest ograniczony - przy włączonej opcji Kąty szczególne - podawane są wartości dokładne.
• Więcej informacji dotyczących założeń modelu można uzyskać tu (en)

Sugestie dotyczące wykorzystania

Wskazówki dotyczące wszystkich symulacji zawarte są w informacjach ogólnych.

Więcej porad dotyczących korzystania z symulacji z uczniami można znaleźć na stronach PhET w sekcji Wskazówki dotyczące korzystania z PhET.

Przykładowe polecenia

• Korzystając ze wzoru na długość okręgu, znajdź długość okręgu jednostkowego. Jaki to ma związek z radianami?
• Zminimalizuj panel Wartości i oszacuj współrzędne punktu na okręgu. Rozwiń panel Wartości, aby sprawdzić swoją odpowiedź. Włącz siatkę, aby sobie ułatwić zadanie!
• Jak wygląda wykres każdej funkcji trygonometrycznej poza widokiem w tej symulacji? Skąd to wiesz?
• Włącz opcję Kąty szczególne i pobaw się symulatorem. Zapisz wszelkie zaobserwowane przez siebie prawidłowości.
• Pozostań w pierwszej ćwiartce i włącz Etykiety. Wykorzystaj swoją wiedzę na temat trygonometrii trójkąta prostokątnego, aby wyjaśnić, dlaczego \(\sin\theta = y\), \(\cos\theta =x\), \(\tan\theta = \frac{y}{x}\).
• Określ znak (dodatni lub ujemny) dla \(\sin330^{\circ}\), \(\cos205^{\circ}\) i \(\tan112^{\circ}\)
• Określ wartość \(\theta\) dla następujących par współrzędnych: \((\frac{1}{2},\frac{\sqrt{3}}{2})\), \((-\frac{1}{2},-\frac{\sqrt{3}}{2})\), \((\frac{\sqrt{3}}{2},-\frac{1}{2})\), \((-\frac{\sqrt{3}}{2},\frac{1}{2})\).

Zobacz wszystkie opublikowane na stronach PhET aktywności dla Funkcje trygonometryczne tutaj (dostęp do materiałów wymaga zalogowania).