Ruch obiegowy Ziemi wokół Słońca

Zagadnienia

• Ruch obiegowy Ziemi
• Nachylenie osi ziemskiej
• Zmiany oświetlenia Ziemi

Opis

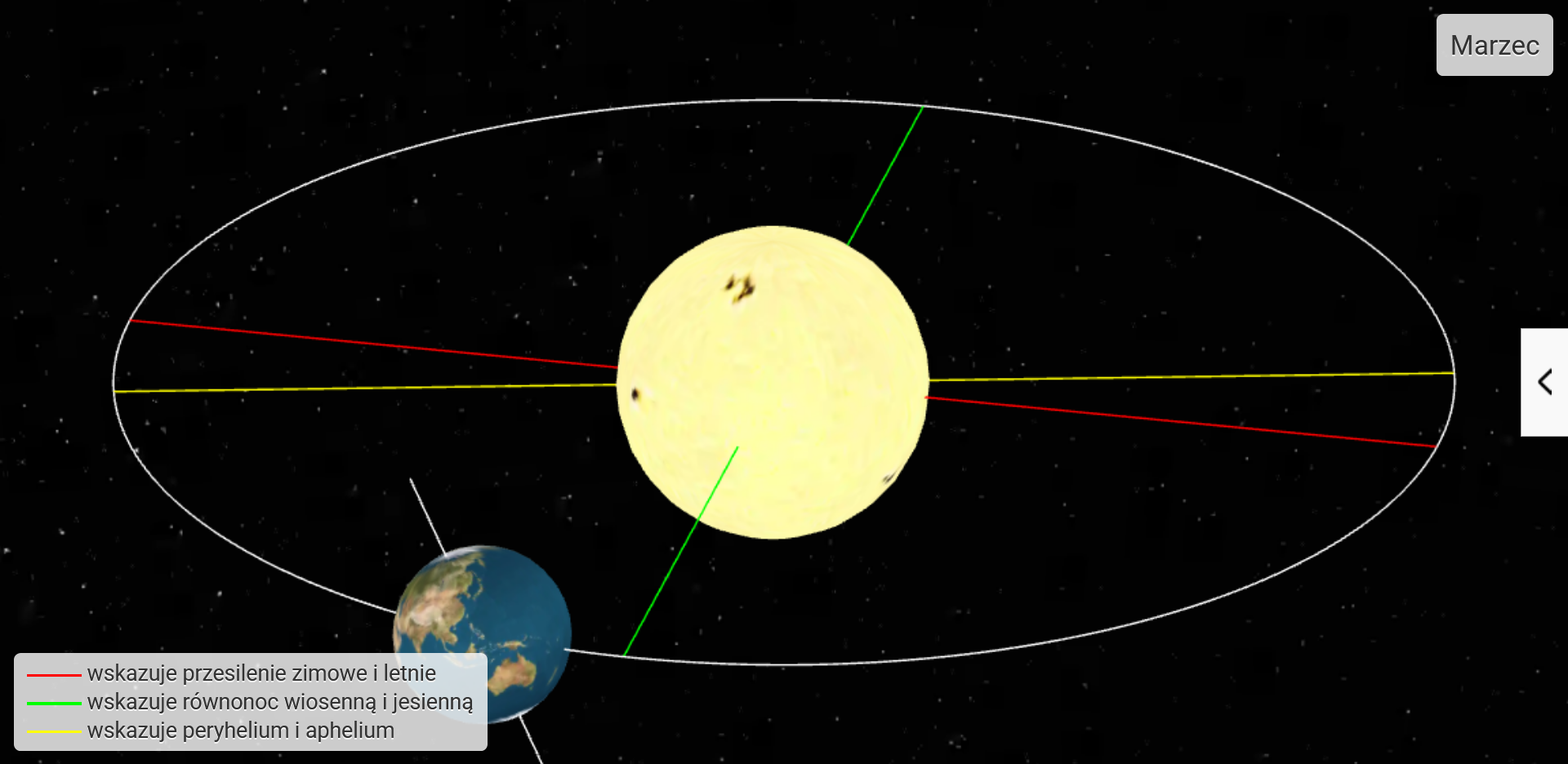
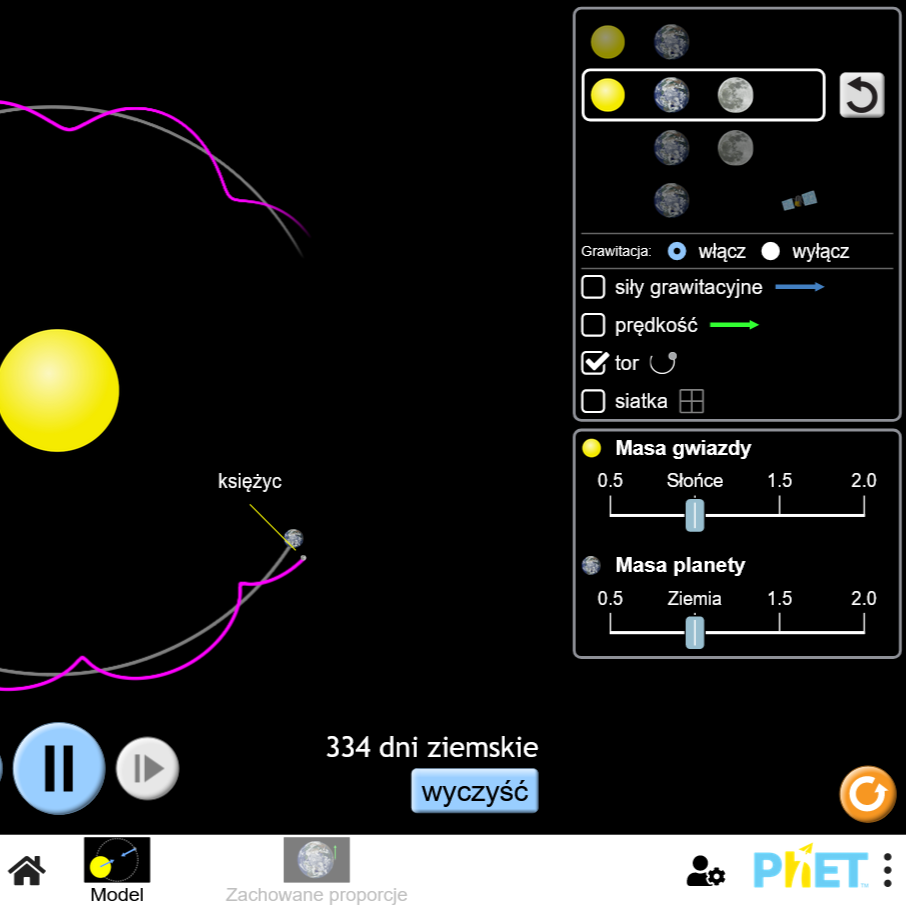
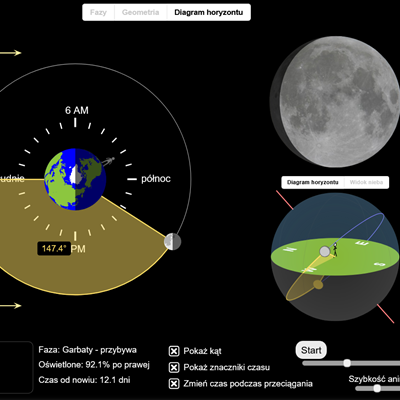
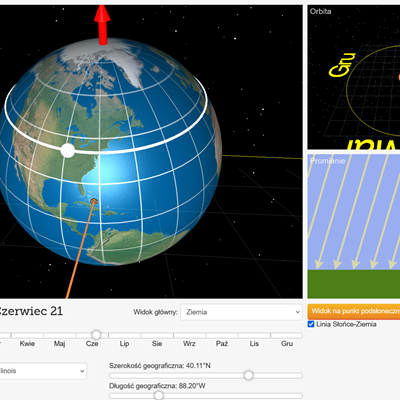
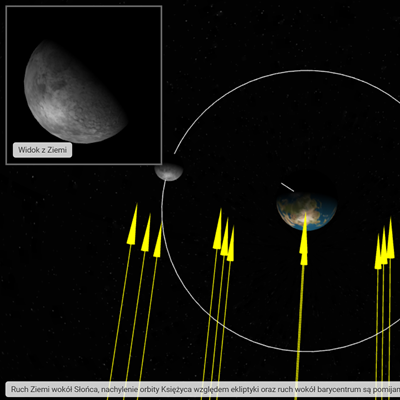
Jak wygląda orbita Ziemi wokół Słońca? Co spowodowałaby większa ekscentryczność toru? Interaktywna animacja obrazująca tytułowe zagadnienie.

© Václav Černík 2017–2021 (tłumaczenie edukator.pl) Źródło: https://www.earthspacelab.com/

W szablonie strony niniejszych instrukcji wykorzystano kod html/css: phydemo.app.

Poziom

Szkoła podstawowa, Szkoła średnia

Przykładowe cele nauczania

• Własności ruchu obiegowego Ziemi wokół Słońca
• Wyjaśnienie pojęć aphelium i peryhelium
• Ocena wpływu ekscentryczności orbity na ilość docierającej energii.

Przykładowe materiały teoretyczne

• Ruch obiegowy Ziemi (Wikipedia)
• Ruch obiegowy Ziemi (Zintegrowana platforma edukacyjna)
• Następstwa ruchu obiegowego Ziemi (Zintegrowana platforma edukacyjna)

Sterowanie symulacją

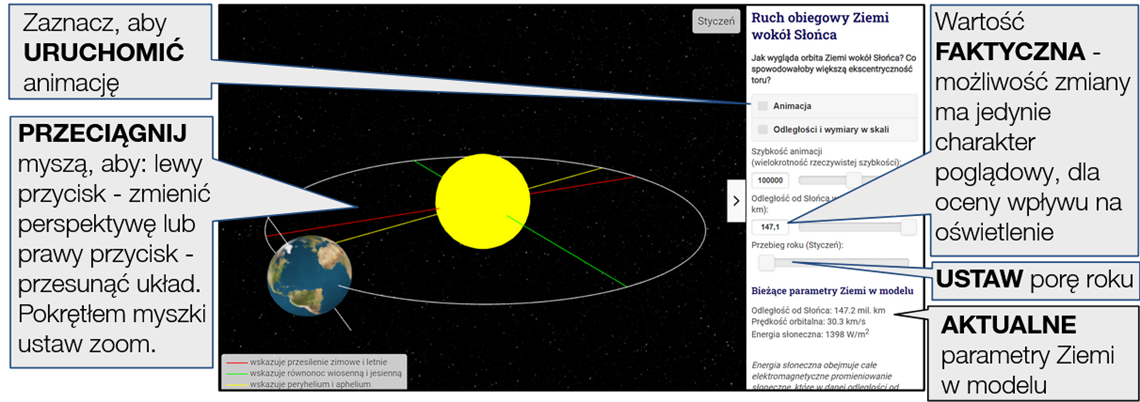
Sterowanie symulacją jest intuicyjnie proste i nie wymaga komentarza. Domyślne ustawienia są zgodne z wartościami rzeczywistymi. Przeciągając myszką, można zmieniać perspektywę. Pokrętłem myszki można ustawić zoom.

Uproszczenia modelu

• Rozmiary Ziemi i Słońca, oraz ich odległość w animacji są czysto umowne. Skala odległości nie jest zachowana.
• Domyślnie ustawiona odległość Ziemi w peryhelium od Słońca, 147,1 mln km, jest zgodna z faktyczną. Jeśli chcemy przyjrzeć się rzeczywistym parametrom ruchu Ziemi, nie należy zmieniać tej odległości (jeżeli została zmieniona, należy ustawić ją zgodnie z wartością faktyczną - ręcznie suwakiem lub ponownie załadować ramkę lub stronę). Możliwość zmiany tego parametru, tu w symulacji, ma jedynie charakter poglądowy, żeby umożliwić ocenę, jaki to miałoby wpływ na energię słoneczną docierającą do Ziemi.
• Szybkość animacji można regulować i jest ona wielokrotnością rzeczywistej szybkości.

Sugestie dotyczące wykorzystania

Wskazówki dotyczące wszystkich symulacji zawarte są w informacjach ogólnych.

Więcej porad dotyczących korzystania z symulacji z uczniami można znaleźć na stronach PhET w sekcji Wskazówki dotyczące korzystania z PhET.

Przykładowe polecenia

• Obejrzyj animację ruchu Ziemi wokół Słońca z domyślną odległością od Słońca ustawioną na rzeczywistą. Jaka jest odległość Ziemi od Słońca w aphelium?
• Jaka jest prędkość Ziemi w peryhelium, a jaka w aphelium?
• Jak zmienia się energia słoneczna padająca na powierzchnię 1 m² ustawioną prostopadle do promieni słonecznych w ciągu roku? Jaki to ma związek z porami roku?
• Opisz kształt orbity Ziemi wokół Słońca. Następnie dostosuj odległość Ziemi od Słońca na rysunku (ustaw mniejszą wartość). Jak zmienia się kształt orbity? Jaki ma to wpływ na prędkość ruchu orbitalnego i energię słoneczną w ciągu roku? Omów, jakie może to mieć konsekwencje dla życia na Ziemi.

Interaktywne arkusze ćwiczeń

Należy traktować je jako szablon. Zalogowany uczestnik może kopiować je do swoich materiałów (Testy) i tu dowolnie remiksować dostosowując do swoich potrzeb. Link na górze po prawej

Testy, pytania sprawdzające

1. Ziemia obiega Słońce po orbicie zbliżonej do okręgu w odległości ok. 150 mln km. Z punktu widzenia obserwatora patrzącego na północną półkulę porusza się w kierunku:
   • zgodnym z ruchem wskazówek zegara.
   • przeciwnym do ruchu wskazówek zegara.
2. W rzeczywistości tor ruchu Ziemi ma kształt elipsy - odległość Ziemi od Słońca zmienia się w niewielkim zakresie. Zmiany te możesz obserwować po prawej stronie w Bieżące parametry Ziemi w modelu. Punkt na orbicie okołosłonecznej, znajdujący się w miejscu największego zbliżenia do Słońca nosi nazwę peryhelium i dla Ziemi jego odległość wynosi 147,1 mln km. Punkt położony najdalej to aphelium i dla Ziemi jego odległość w km wynosi (wpisz samą liczbę w zaokrągleniu do miliona, nie wpisuj jednostek)
3. Wraz ze wzrostem odległości Ziemi od Słońca:
   
   

   	maleje	rośnie	nie zmienia się
   wartość prędkości jej ruchu liniowego
   energia słoneczna docierająca do niej w jednostce czasu
   nachylenie osi ziemskiej

   
   
4. Minimalna wartość prędkości ruchu liniowego Ziemi w ruchu obiegowym wokół Słońca wynosi około
   • 29,3 km/s i jest osiągana gdy Ziemia mija aphelium
   • 29,3 km/s i jest osiągana gdy Ziemia mija peryhelium
   • 8 m/s i jest osiągana gdy Ziemia mija aphelium
   • 8 m/s i jest osiągana gdy Ziemia mija peryhelium
   • 30,3 km/s i jest osiągana gdy Ziemia mija aphelium
   • 30,3 km/s i jest osiągana gdy Ziemia mija peryhelium
   • 15,7 km/s i jest osiągana gdy Ziemia mija aphelium
   • 15,7 km/s i jest osiągana gdy Ziemia mija peryhelium
5. Na skutek zmian odległości Ziemi od Słońca, zmienia się nieco wielkość energii słonecznej docierającej do Ziemi. W symulacji, w Bieżących parametrach wyświetlana jest aktualna wartość energii słonecznej, która w danej odległości od Słońca pada w ciągu 1 s na powierzchnię 1 m² prostopadłą do promieni słonecznych (poza atmosferą Ziemi). Wielkość ta dla odległości 1 au (jednostka astronomiczna - w przybliżeniu równa średniej odległości Ziemi od Słońca) wynosi około 1367 W/m² i jest nazywana stałą słoneczną.
   Oceń przwdziwość zdania:
   Procentowe zmiany tej energii (w stosunku do stałej słonecznej) nie przekraczają 5% i nie mają znaczącego związku z porami roku.
   • FAŁSZ
   • PRAWDA
6. A teraz sprawdzimy, oczywiście czysto hipotetycznie, co byłoby, gdyby odległość Ziemi w peryhelium od Słońca była inna (ustaw najmniejszą możliwą tu w symulacji wartość 60 mln km - zwiększamy tu pewien parametr elipsy, nazywany mimośrodem lub ekscentrycznością). Przyjrzyj się teraz, jak zmieniłby się kształt toru i jaki miałoby to wpływ na prędkość ruchu obiegowego i energię słoneczną docierającą do powierzchni tej wydumanej planety, w miarę upływu roku planetarnego.
   Zaznacz poprawne odpowiedzi.
   
   

   	2 razy większa	4 razy większa	6 razy większa	16 razy większa	2 razy mniejsza	4 razy mniejsza	6 razy mniejsza	16 razy mniejsza
   Maksymalna odległość tej planety od Słońca, w porównaniu do odległości minimalnej, jest około
   Wartość prędkości liniowej ruchu obiegowego, gdy ta planeta znajduje się najdalej od Słońca, w porównaniu do tej, którą ma, gdy jest najbliżej, jest około
   Maksymalna energia słoneczna, docierająca do planety w ciągu 1 s, w porównaniu do minimalnej, jest około
   Energia słoneczna, która pada w ciągu 1 s na powierzchnię 1 m2 prostopadłą do promieni słonecznych w peryhelium planety, w porównaniu do naszej stałej słonecznej, jest około

   
   
7. Zaznacz poprawne odpowiedzi.
   
   W przypadku planety krążącej wokół gwiazdy po silnie spłaszczonej elipsie,
   

   	znacznie się zmienia	nieznacznie się zmienia	pozostaje stała
   jej odległość od gwiazdy, w ciągu roku planetarnego (okresu obiegu)
   odległość apocentrum (punkt orbity najbardziej oddalony od gwiazdy) od gwiazdy
   wartość prędkości liniowej ruchu obiegowego
   wartość energii promieniowania gwiazdy, docierającego do planety w ciągu 1 sekundy

   
   

Symulacje zbliżone tematycznie