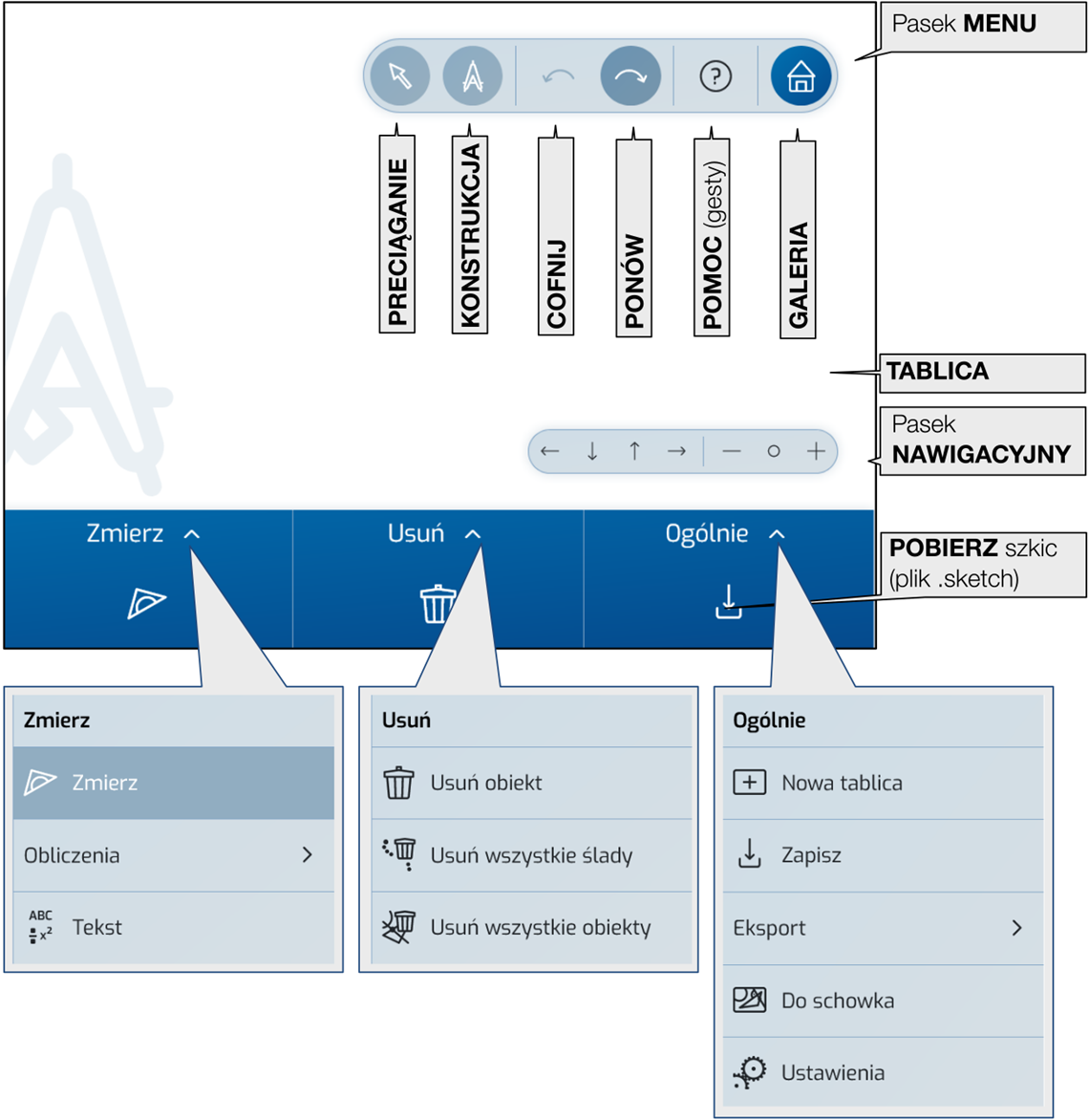
Opis aplikacji i instrukcje dotyczące wykonywania podstawowych zadań w sketchometry.
Sketchometry to dynamiczne oprogramowanie matematyczne do geometrii euklidesowej i wykresów funkcji. Natychmiast przekształca odręczne rysunki w interaktywne konstrukcje geometryczne, które mogą być przeciągane i modyfikowane. Użytkownik szkicuje punkty, okręgi i linie na ekranie, a sketchometry jest w stanie zinterpretować te kreski i przetworzyć na dokładne obiekty geometryczne. (© 2011 - 2024 | Center for Mobile Learning with Digital Technology, University of Bayreuth).
Dynamiczne oprogramowanie matematyczne do wizualizacji relacji geometrycznych jest z powodzeniem stosowane na lekcjach matematyki od wielu lat. Sketchometry to oprogramowanie oparte na gestach, które pozwala szybko i łatwo tworzyć i eksplorować interaktywne konstrukcje za pomocą palca na tablecie, smartfonie lub multimedialnej tablicy. Innowacyjne sterowanie gestami zamienia urządzenia mobilne w elektroniczne narzędzie do szkicowania, z którego można korzystać bezpośrednio w klasie. Sketchometry jest dostępne bezpłatnie jako aplikacja lub bezpośrednio jako wersja na żywo (kod QR) w przeglądarce. Dostępne w kilku językach, w tym po polsku! Konstrukcje można wygodnie zapisywać w chmurze lub na komputerze.
Krótki, zwięzły i przejrzysty – informator i jednocześnie warsztat sketchometry Geometria palcem wyjaśnia krok po kroku, jak używać sketchometry jako narzędzia do szkicowania na lekcjach geometrii.
Podstawowe gesty są szczegółowo wyjaśnione na praktycznych przykładach. Podano również informacje ogólne na temat nauczania i uczenia się za pomocą sketchometry.
W opracowaniu niniejszego poradnika wykorzystano materiały Sketchometry.
W szablonie strony wykorzystano kod html/css: phydemo.app.
Narzędzie jest bardzo intuicyjne i już po kilku minutach jesteśmy w stanie skutecznie bawić się geometrią, wykorzystując jego podstawowe możliwości i, w miarę używania, rozszerzać je o bardziej zaawansowane funkcjonalności.
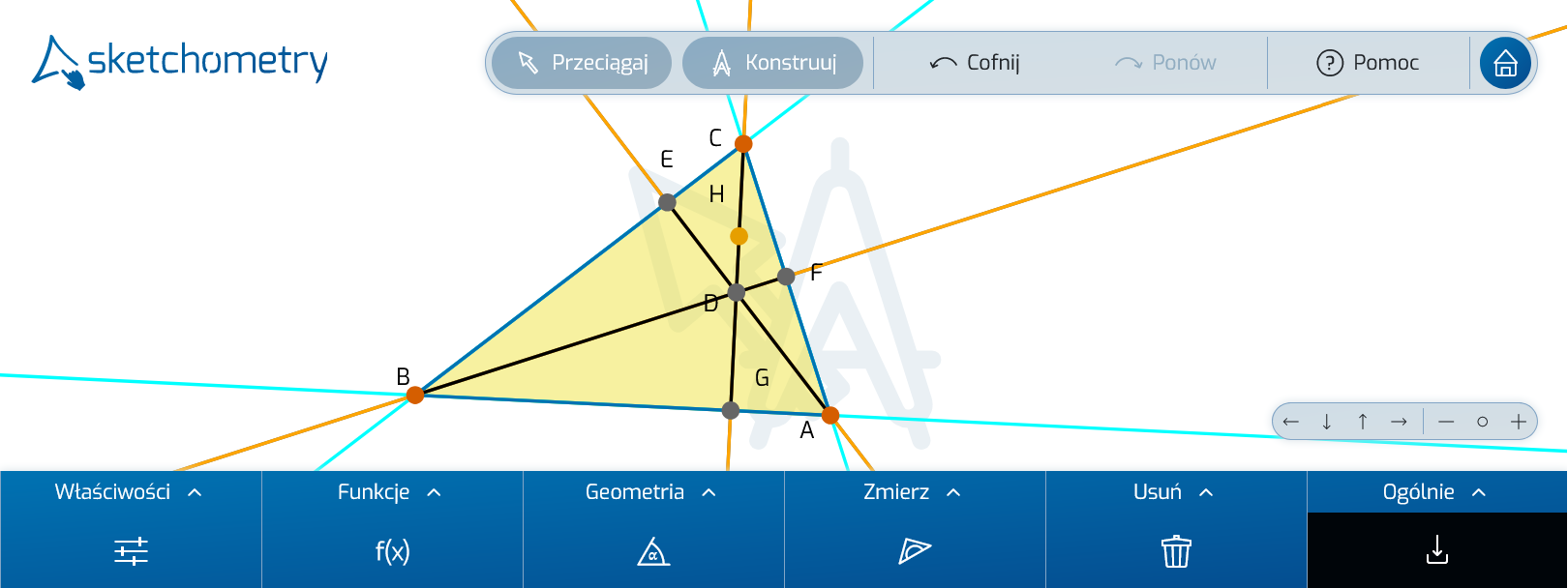
Tablica to podstawowy element sketchometry. Tu za pomocą odpowiednich gestów i dodatkowych narzędzi tworzymy konstrukcje geometryczne. Poszczególne tablice/konstrukcje automatycznie zapisywane są w Galerii. Na środku tablicy w tle pokazywany jest symbol wybranego aktualnie narzędzia/trybu pracy.

Tu, oprócz paska narzędziowego, widoczny jest pasek menu i nawigacyjny. Ten układ interfejsu można dowolnie zmieniać w ustawieniach, dostosowując go do swoich potrzeb.

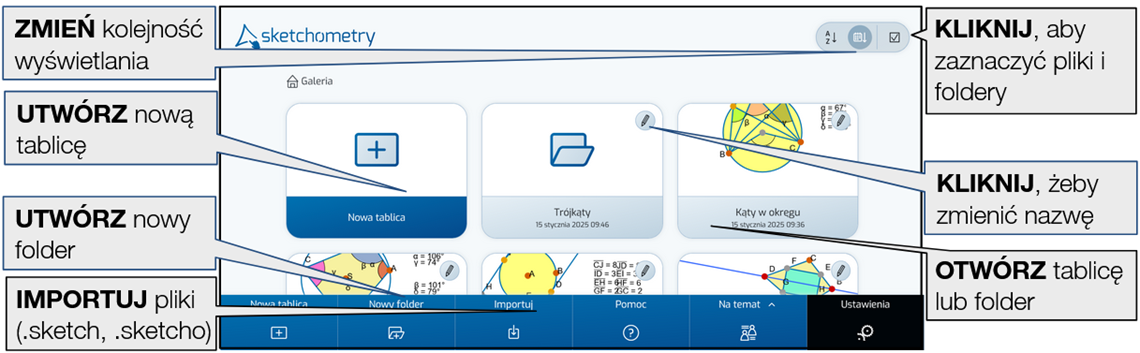
Kliknięcie ikony z domem przenosi nas do galerii. W galerii zapisane są wszystkie foldery i tablice, które utworzyliśmy. Tablice zapisują się automatycznie ale jeśli wyczyścimy przeglądarkę, pliki zostaną usunięte, o ile nie zaznaczymy, że mają być zachowane. Dlatego jeśli chcemy je zachować na dłużej lub udostępnić, należy szkic pobrać w postaci pliku .sketcho.
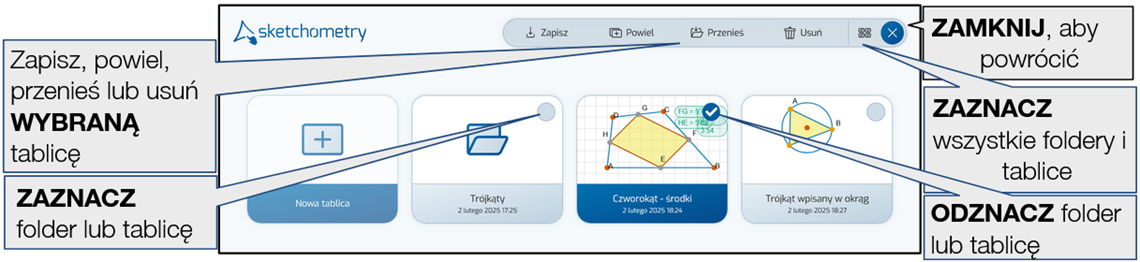
Zamiast przycisku Wybierz można od razu zaznaczyć folder lub tablicę, klikając na nim prawym przyciskiem myszy.
Warsztat ten wprowadza krok po kroku do koncepcji i daje przykłady wykorzystania sketchometry na zajęciach z geometrii. Jego ukończenie zajmuje około 90 minut.
Dla każdego z poszczególnych przykładów używana jest nowa plansza, którą można otworzyć w galerii sketchometry poprzez  Nowa tablica.
Nowa tablica.
Dostęp do galerii sketchometry można uzyskać za pomocą ikony  na pasku menu.
na pasku menu.

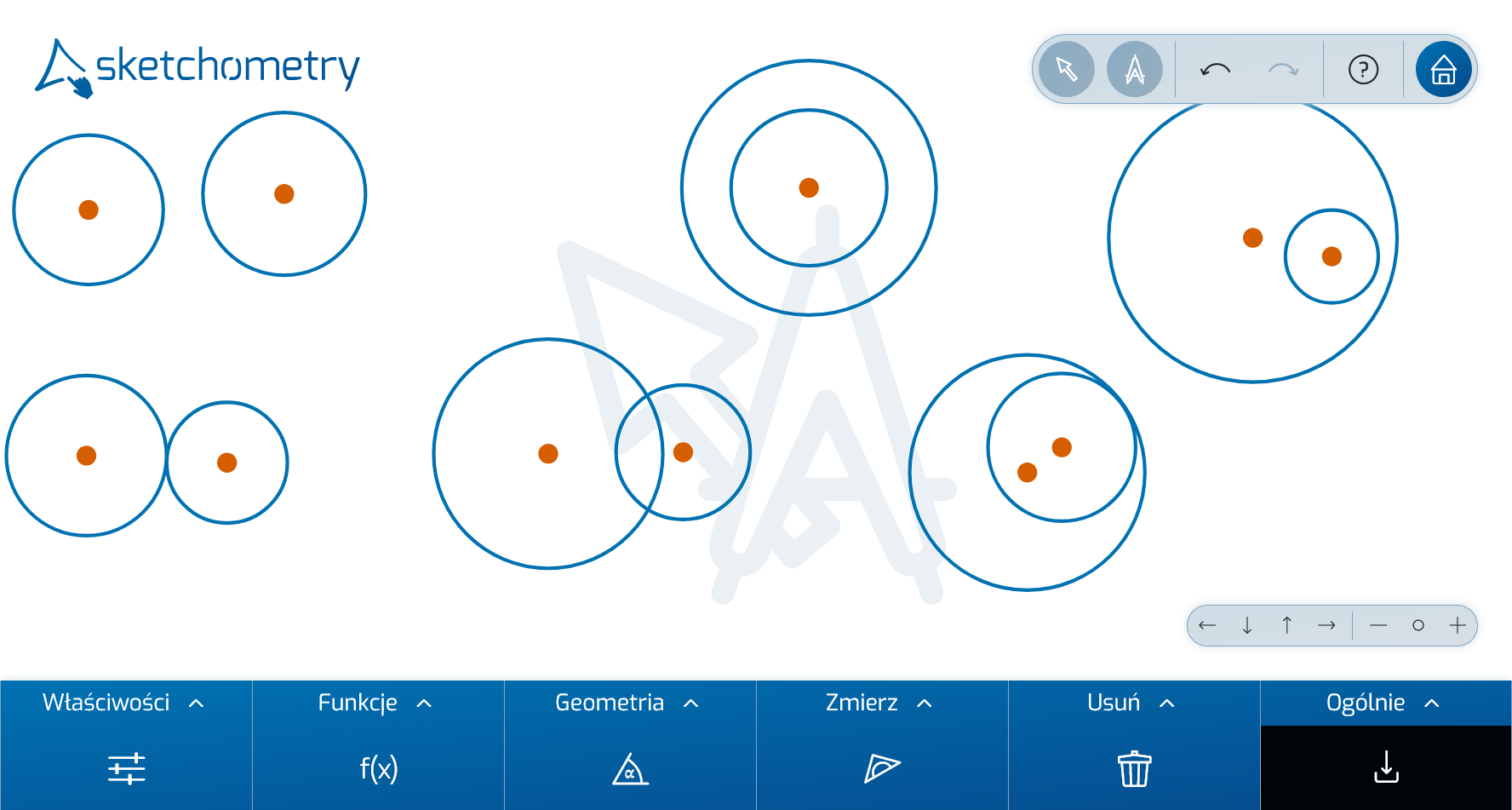
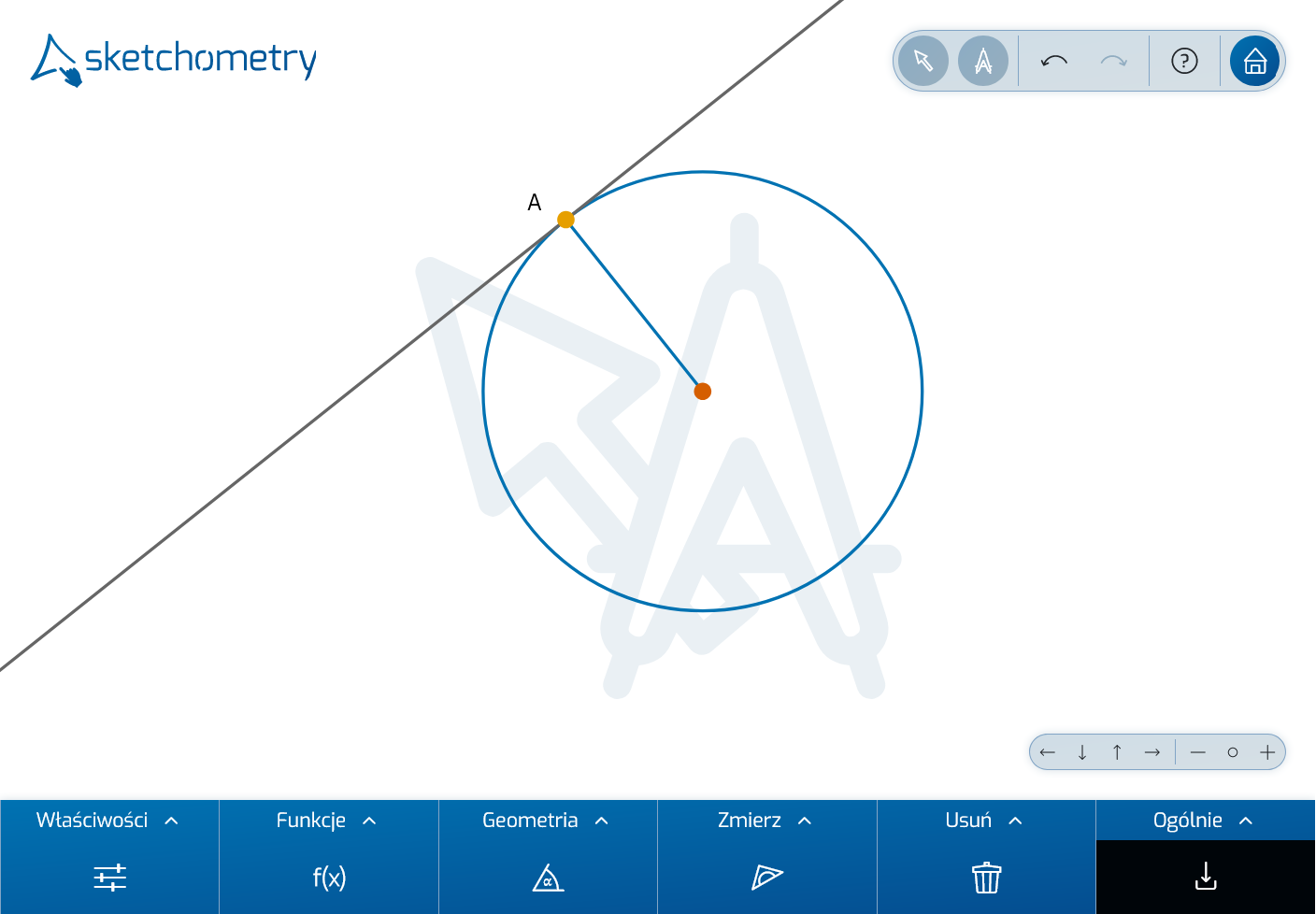
Naszkicuj okrąg palcem lub za pomocą myszy na tablicy. Nazwa rozpoznanego obiektu - Okrąg jest wyświetlana na pasku informacyjnym. Gdy tylko podniesiesz palec, pojawi się okrąg i jego środek.
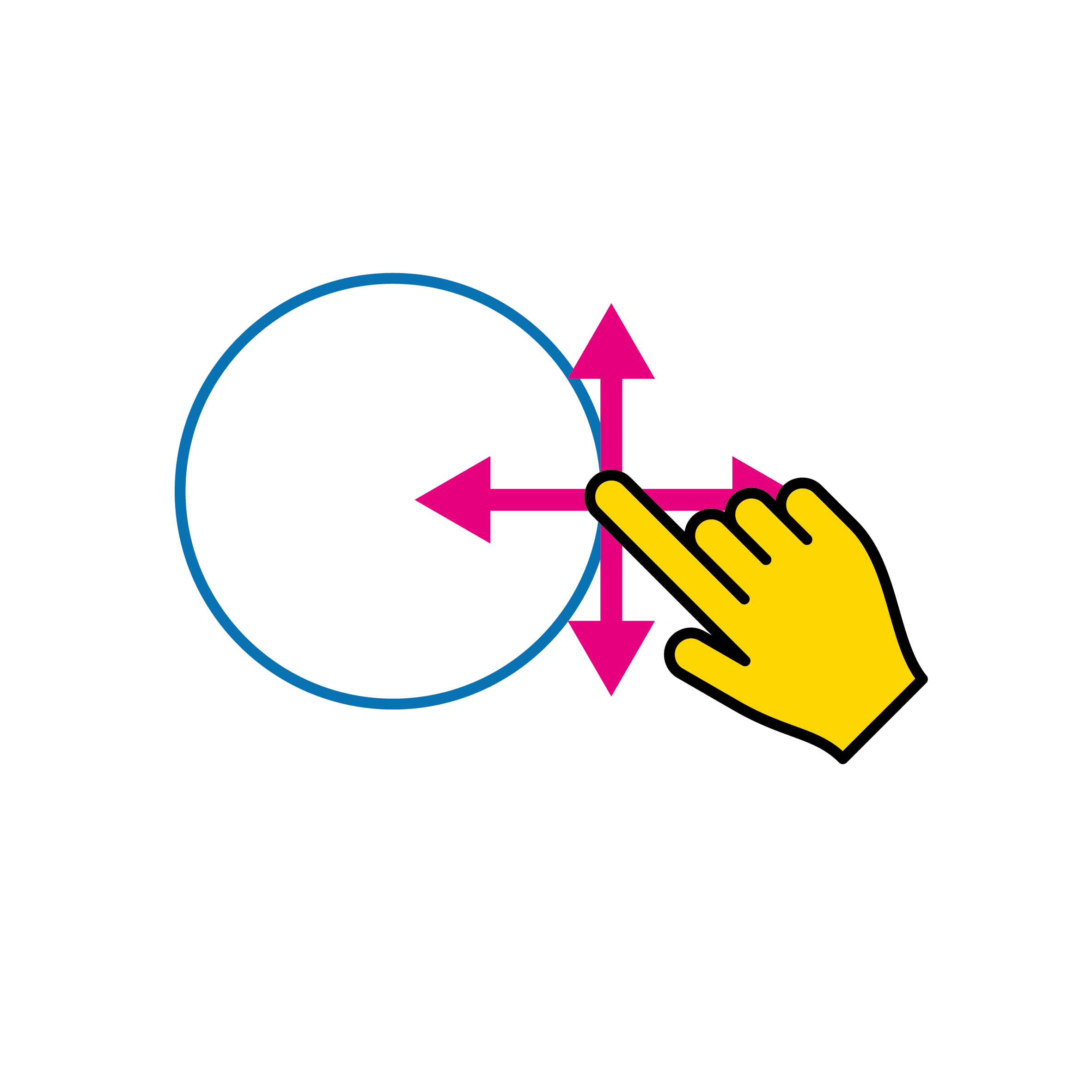

Szczególna cecha sketchometry: Nie trzeba wcześniej wybierać własnego narzędzia okrąg. sketchometry automatycznie rozpoznaje szkic palcem (= gest). Położenie okręgu można zmienić palcem, przeciągając linię okręgu lub punkt środkowy. Rozmiar okręgu można zmienić dwoma palcami: Dotknij linii okręgu w dwóch punktach i przesuń palce do siebie lub od siebie, podobnie jak podczas powiększania zdjęć na smartfonie.
 Przeciąganie i
Przeciąganie i  Konstruowanie Mogą być one używane niezależnie. Aktualnie aktywne narzędzie jest podświetlone na pasku menu i wyświetlane w tle tablicy. Na początek zaleca się używanie ich oddzielnie.
Konstruowanie Mogą być one używane niezależnie. Aktualnie aktywne narzędzie jest podświetlone na pasku menu i wyświetlane w tle tablicy. Na początek zaleca się używanie ich oddzielnie. Przeciąganie i Konstruowanie
Przeciąganie i KonstruowanieWstępne doświadczenie można zdobyć, wykonując następujące zadanie:
Przesuwając, powiększając i zmniejszając okręgi, uczniowie obserwują i opisują różne przypadki ich wzajemnego położenia.
Jeśli chcesz cofnąć ostatni krok konstrukcji - na przykład z powodu nieprawidłowego rozpoznania gestu - możesz to zrobić za pomocą opcji ⤺Cofnij na pasku menu.

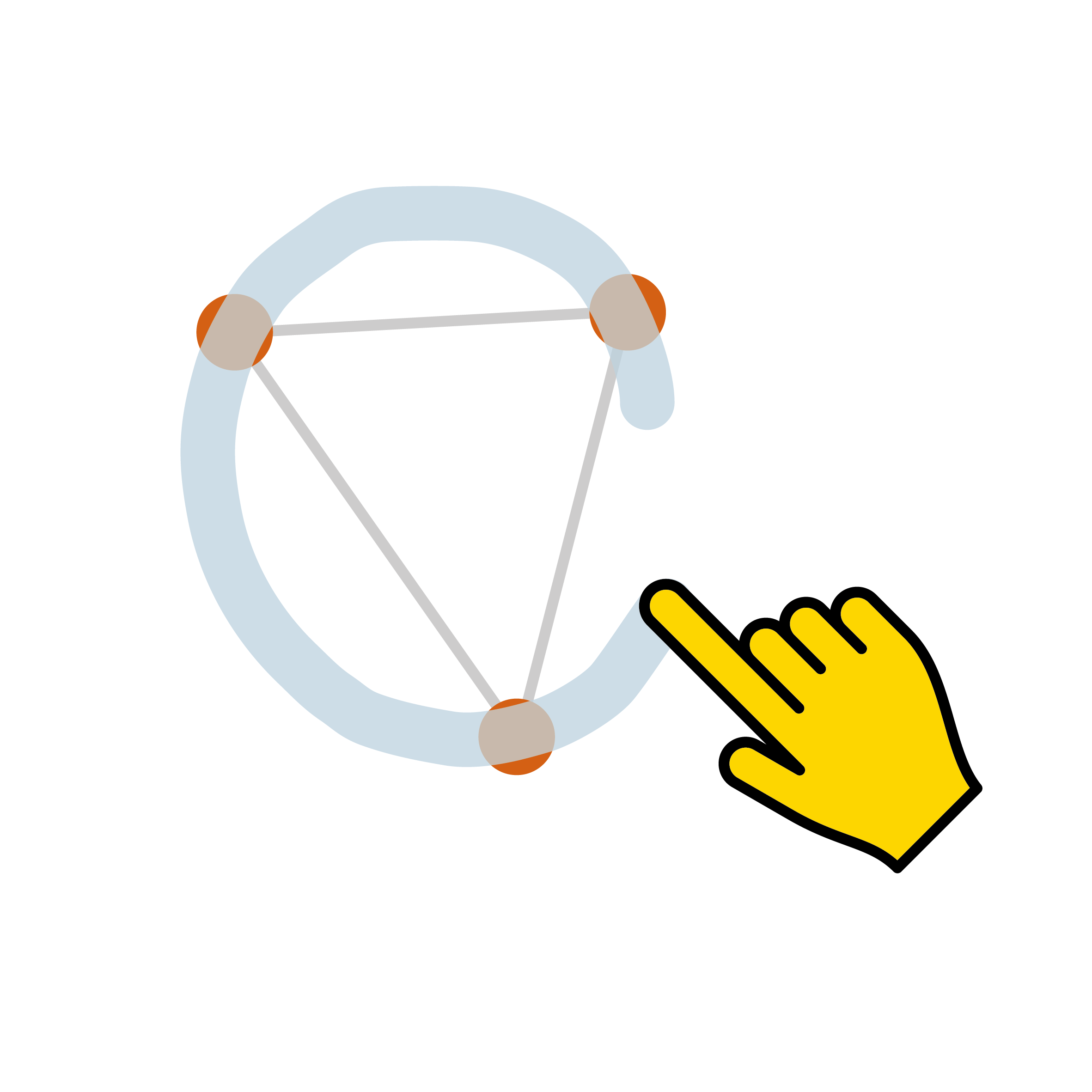
Jednakże sketchometry oferuje jeszcze więcej. Możesz utworzyć okrąg opisany na trójkącie, po prostu go szkicując. Zacznij od trójkąta na nowej planszy, a następnie narysuj okrąg przechodzący przez wierzchołki trójkąta. Upewnij się, że dotykasz palcem trzech wierzchołków. Zostaną one wyróżnione szarym pierścieniem. sketchometry utworzy okrąg (wraz z punktem środkowym) opisany na tym trójkącie.
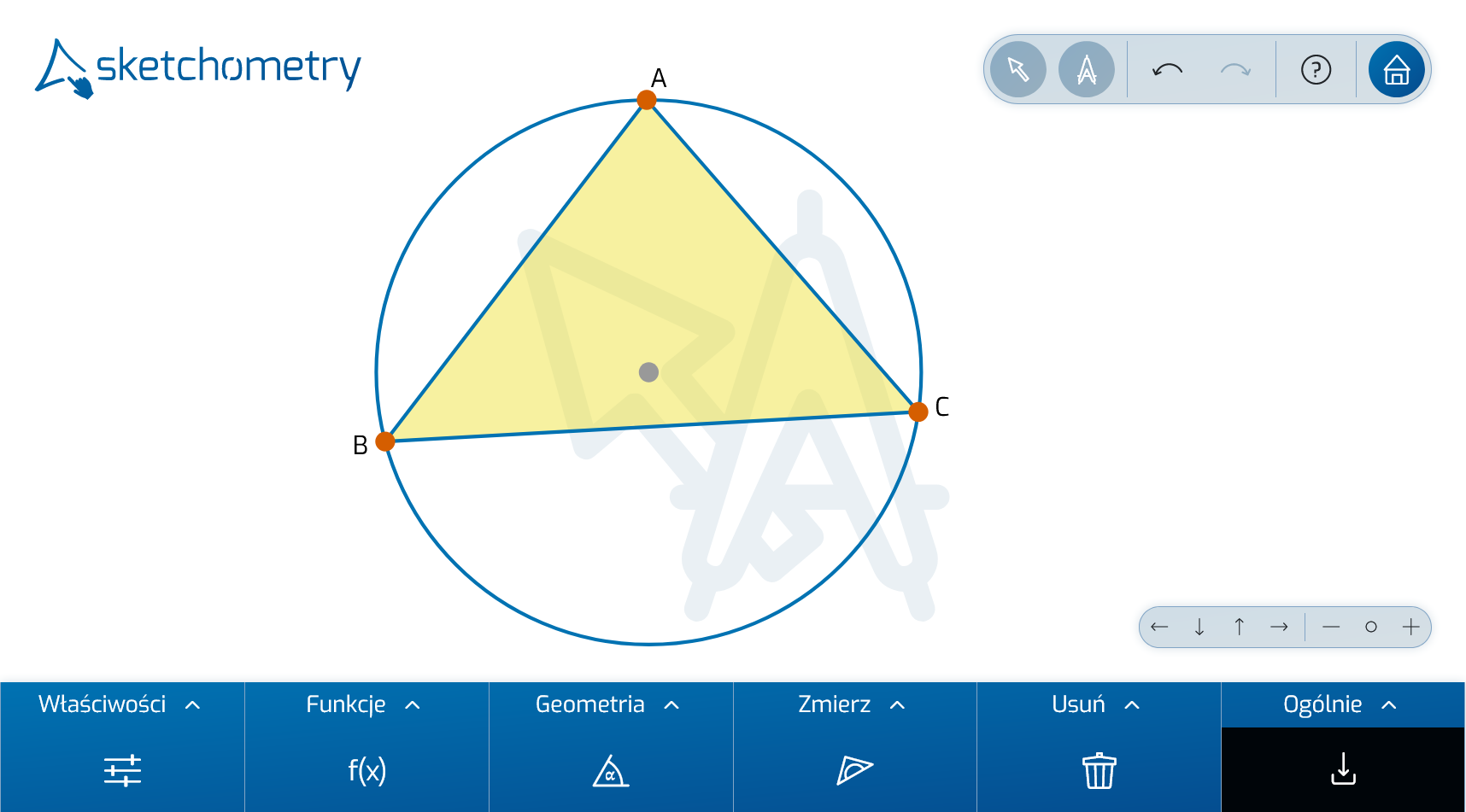
Tutaj również nie jest konieczne wybieranie narzędzia do tworzenia okręgu opisanego. Ten bezpośredni sposób tworzenia okręgu opisanego jest przydatny, jeśli jego konstrukcja i właściwości zostały już omówione na zajęciach, i wtedy na przykład poniższe zadanie można wykonać przy użyciu tej konstrukcji:

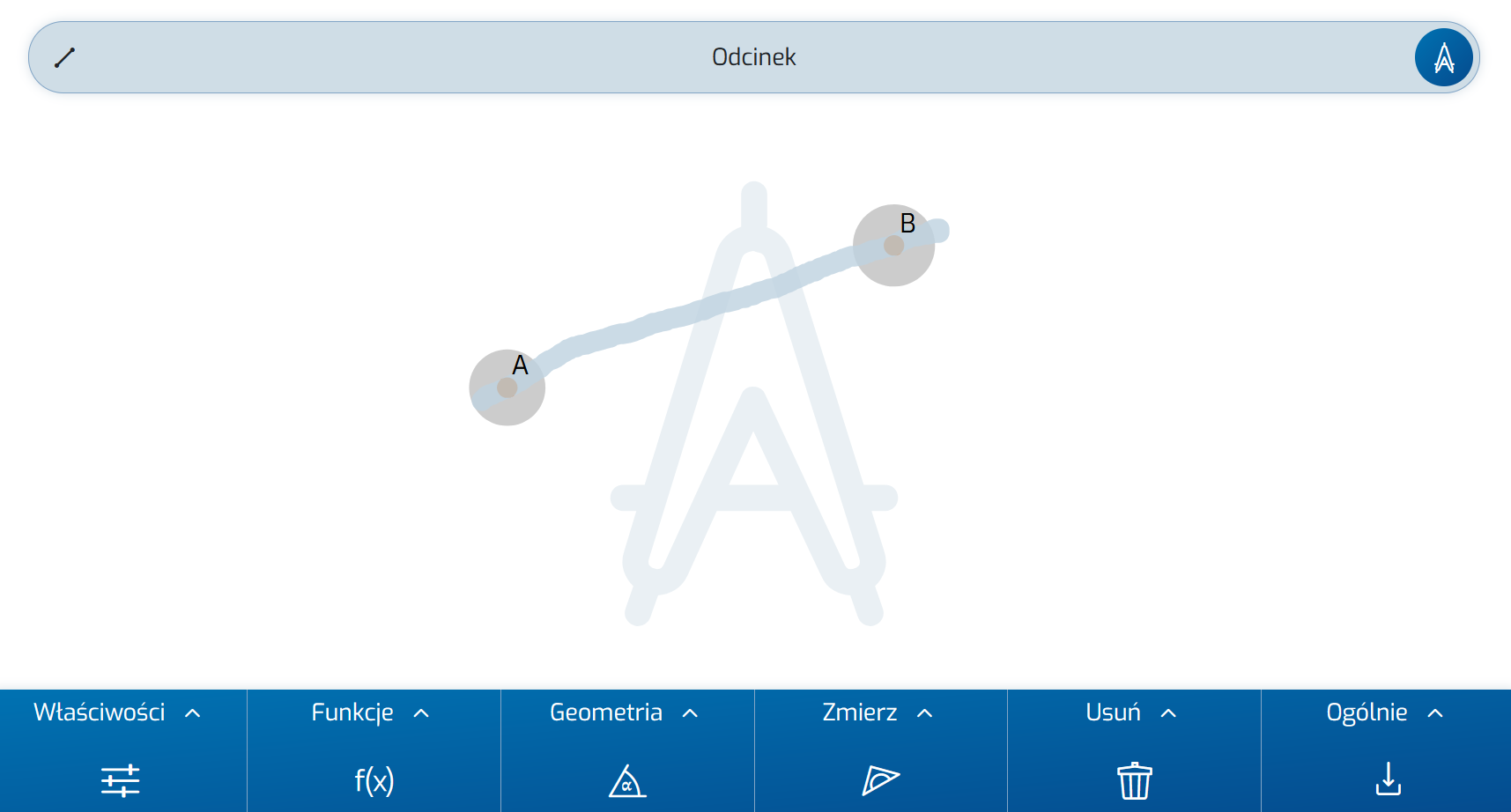
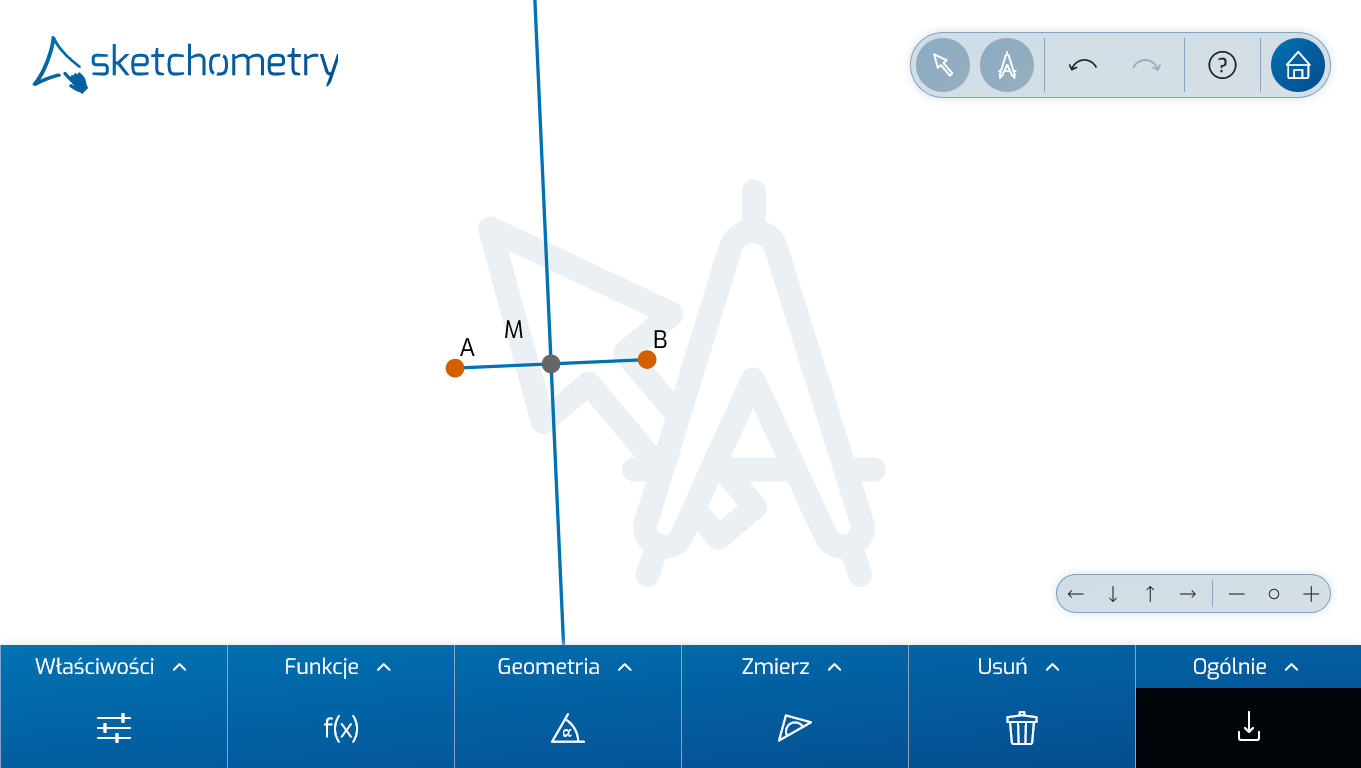
Otwórz nową tablicę i wyłącz funkcję Przeciąganie. Umieść dwa punkty A i B na tablicy i połącz je naszkicowanym odcinkiem. Ponownie upewnij się, że dotykasz obu punktów palcem, aby zostały oznaczone:
Najpierw skonstruuj prostą prostopadłą w klasyczny sposób jako zbiór wszystkich punktów, które są w równej odległości od dwóch podanych punktów: Pierwszy okrąg ze środkiem A przebiega przez punkt B i odwrotnie, drugi okrąg przechodzi wokół punktu B przez punkt A.
Tutaj użyjesz innego gestu. Zacznij od pierwszego okręgu z punktem środkowym A. Gest Okrąg (promień) składa się z dwóch części, które należy naszkicować bez przerywania:

Sketchometry rozpoznaje to jako gest Okrąg (promień) i tworzy okrąg. Okrąg o środku w punkcie B przechodzący przez punkt A jest tworzony w ten sam sposób. W następnym kroku stuknij dwa przecięcia okręgów jeden po drugim, a pojawią się punkty przecięcia. Na koniec naszkicuj linię środkową jako linię prostą przechodzącą przez dwa punkty przecięcia. W przeciwieństwie do gestu Odcinek, zaczynasz wyraźnie przed pierwszym punktem (przecięcia) i kończysz wskazaną linię prostą wyraźnie po drugim punkcie (przecięcia).
 Użyj narzędzia
Użyj narzędzia Własności obiektu, aby ustawić wygląd i zachowanie obiektów.
Własności obiektu, aby ustawić wygląd i zachowanie obiektów. Widoczność, aby pokazać lub ukryć obiekty.
Widoczność, aby pokazać lub ukryć obiekty. Tablica, aby pokazać osie współrzędnych, siatkę lub zmienić kolor tła tablicy. Możesz zmienić położenie paska menu i paska narzędzi lub język za pomocą Interfejsu użytkownika.
Tablica, aby pokazać osie współrzędnych, siatkę lub zmienić kolor tła tablicy. Możesz zmienić położenie paska menu i paska narzędzi lub język za pomocą Interfejsu użytkownika. Widoczność poprzez Właściwości na pasku narzędzi. Stuknij kolejno obiekty, które chcesz ukryć. Po wybraniu innego narzędzia ukryte obiekty znikną całkowicie (ale pozostaną dostępne wewnętrznie). Jeśli w wybranym miejscu znajduje się kilka obiektów, wyświetlona zostanie lista wyboru.
Widoczność poprzez Właściwości na pasku narzędzi. Stuknij kolejno obiekty, które chcesz ukryć. Po wybraniu innego narzędzia ukryte obiekty znikną całkowicie (ale pozostaną dostępne wewnętrznie). Jeśli w wybranym miejscu znajduje się kilka obiektów, wyświetlona zostanie lista wyboru. Widoczność. Ukryte obiekty pojawią się ponownie blade. Stuknij obiekt, który chcesz wyświetlić. Stanie się on ponownie widoczny.
Widoczność. Ukryte obiekty pojawią się ponownie blade. Stuknij obiekt, który chcesz wyświetlić. Stanie się on ponownie widoczny.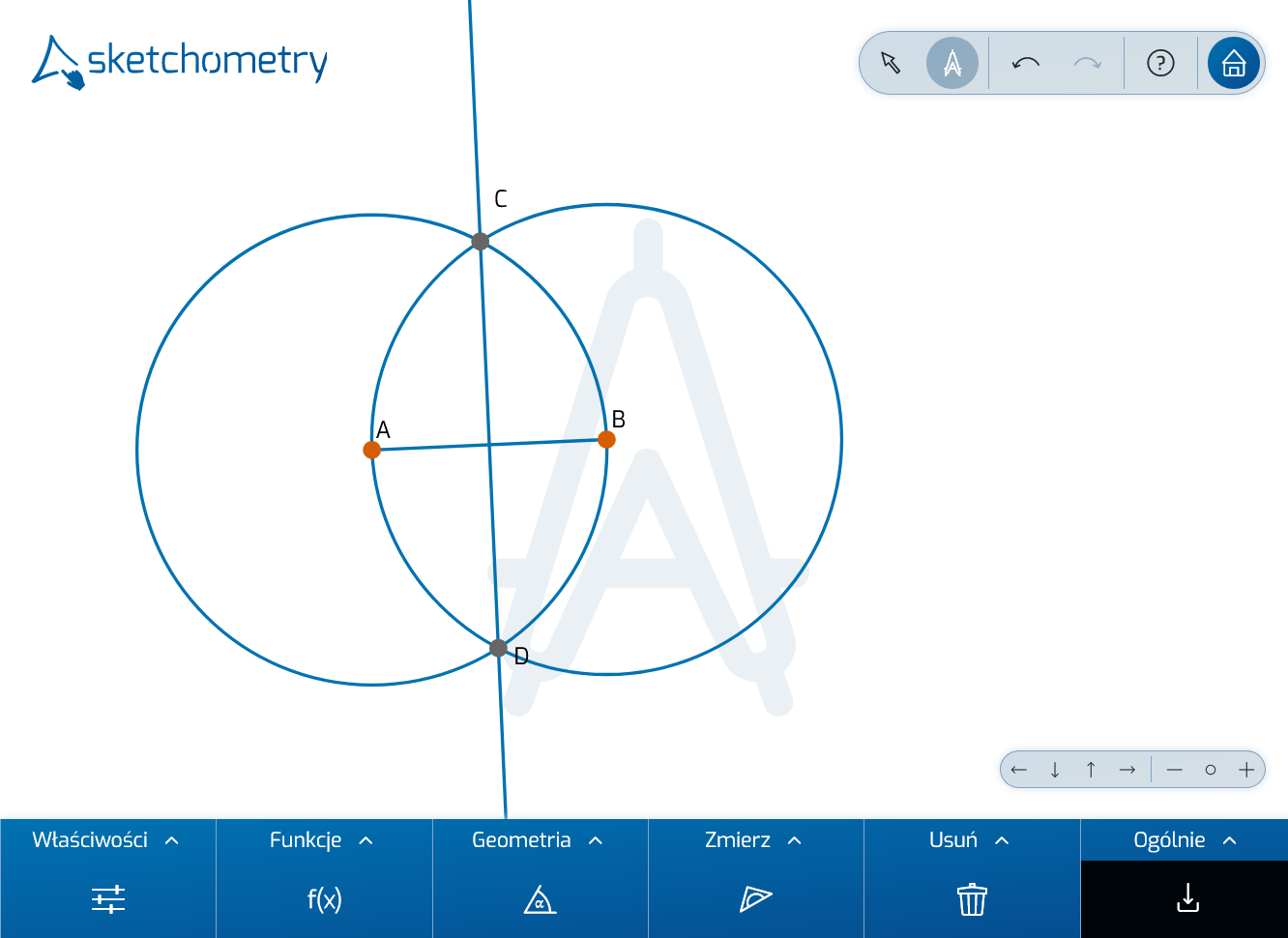
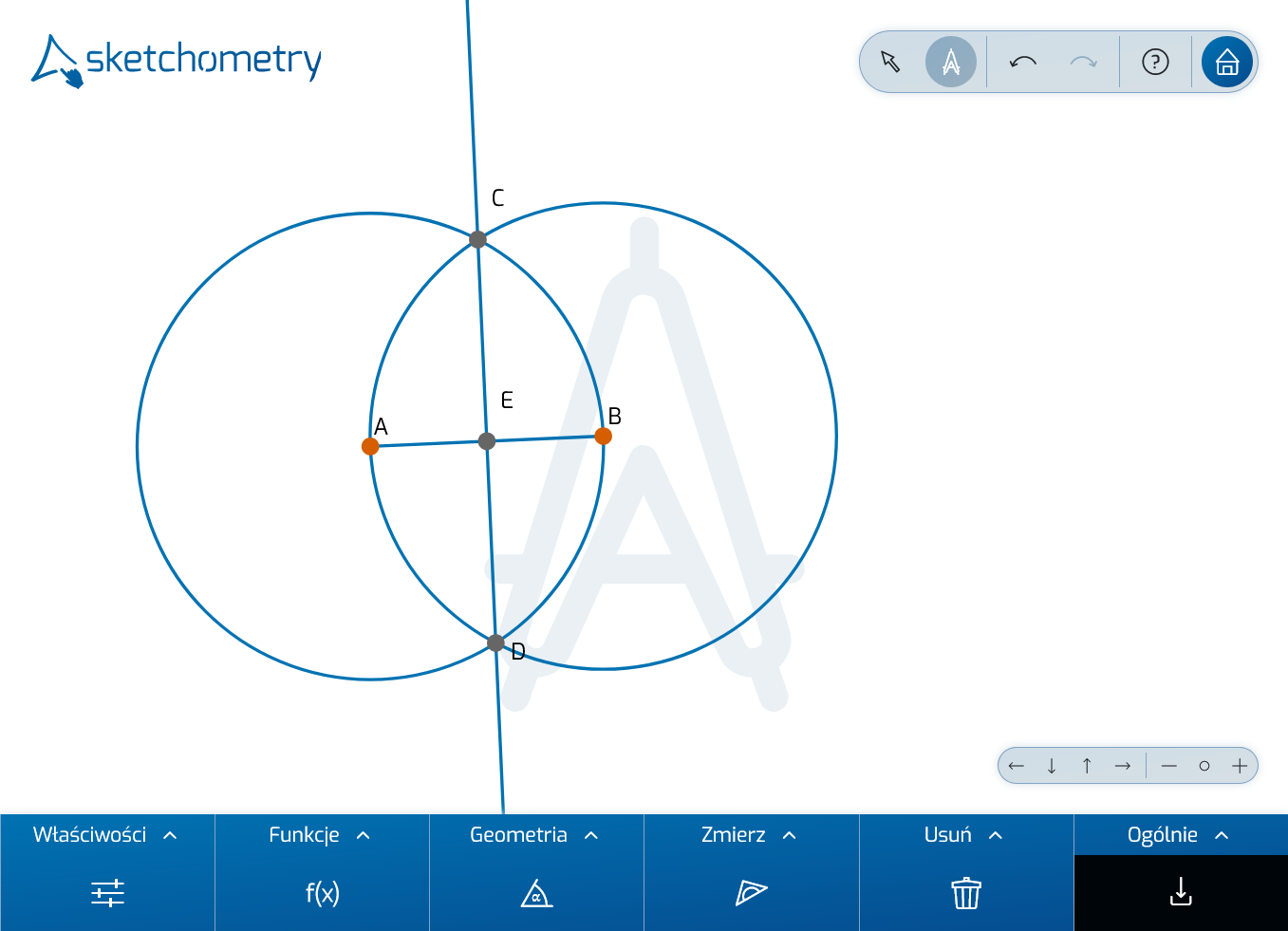
Na koniec zaznacz punkt przecięcia odcinka linią prostopadłą, która dzieli odcinek na pół (symetralna). Sketchometry nazywa aktywnie utworzone punkty alfabetycznie, zaczynając od A. Dlatego ten punkt przecięcia jest oznaczony jako E.
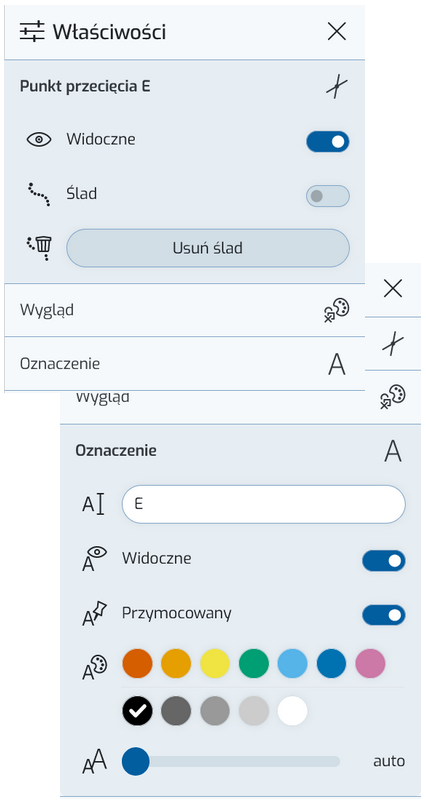
Możesz zmienić nazwę, rozmiar czcionki, ustawienia kolorów i inne właściwości w dowolnym momencie, używając narzędzia  Własności obiektu na pasku narzędzi (poprzez Właściwości). Zmień nazwę punktu E na M. Aby to zrobić, aktywuj narzędzie
Własności obiektu na pasku narzędzi (poprzez Właściwości). Zmień nazwę punktu E na M. Aby to zrobić, aktywuj narzędzie  Własności obiektu i dotknij punktu E. Pojawi się lista wyboru. Wybierz punkt E. sketchometry wyświetla teraz właściwości punktu przecięcia E. Są one podzielone na poszczególne kategorie. Wybierz kategorię Oznaczenie i zmień nazwę E na M.
Własności obiektu i dotknij punktu E. Pojawi się lista wyboru. Wybierz punkt E. sketchometry wyświetla teraz właściwości punktu przecięcia E. Są one podzielone na poszczególne kategorie. Wybierz kategorię Oznaczenie i zmień nazwę E na M.
Zamknij Właściwości za pomocą ✕. Punkt przecięcia oznaczony został teraz literą M.
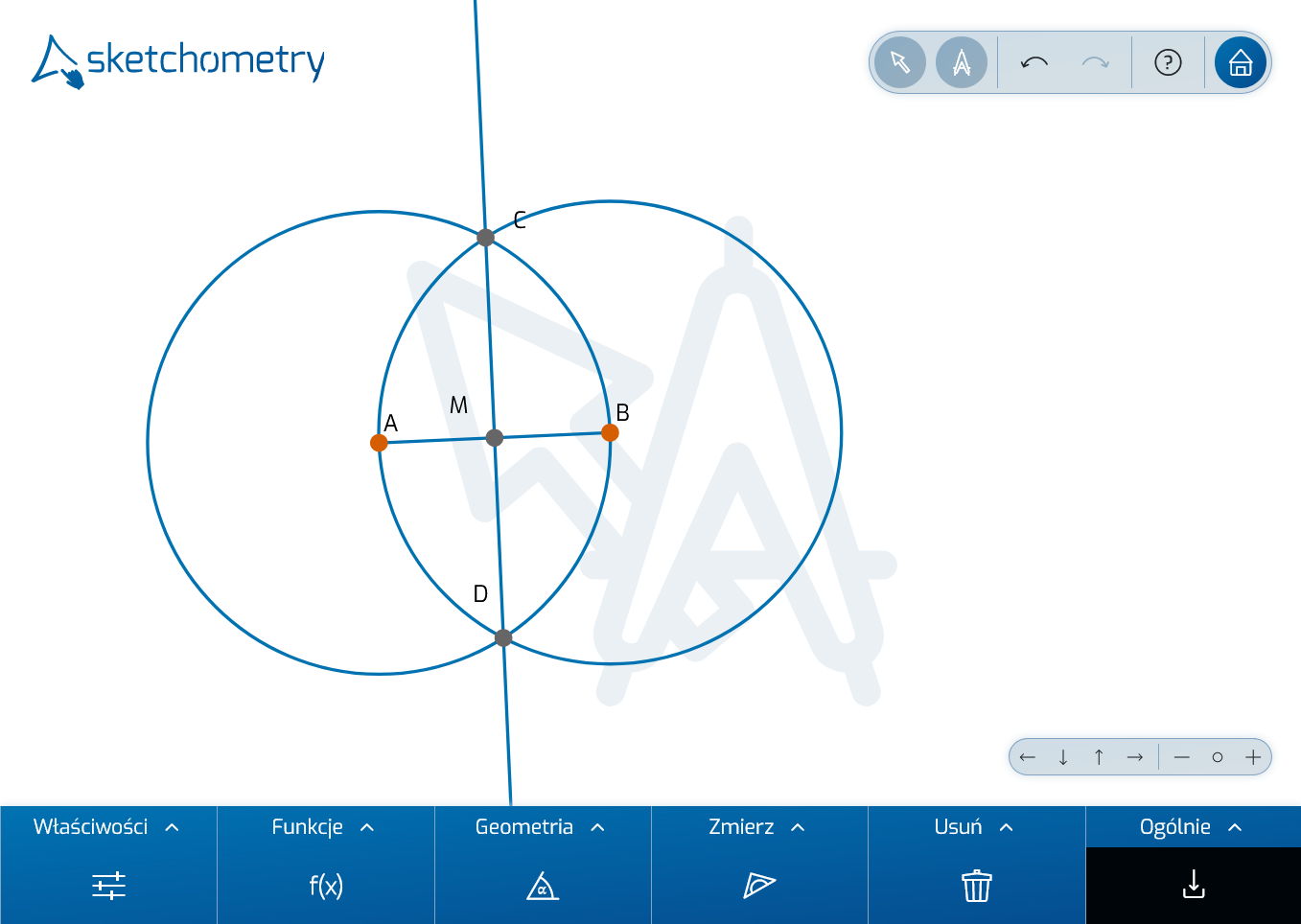
Na koniec ukryj obiekty pomocnicze (tutaj dwa okręgi i ich punkty przecięcia) za pomocą narzędzia  Widoczność. Konstrukcja linii prostopadłej jest teraz ukończona.
Widoczność. Konstrukcja linii prostopadłej jest teraz ukończona.
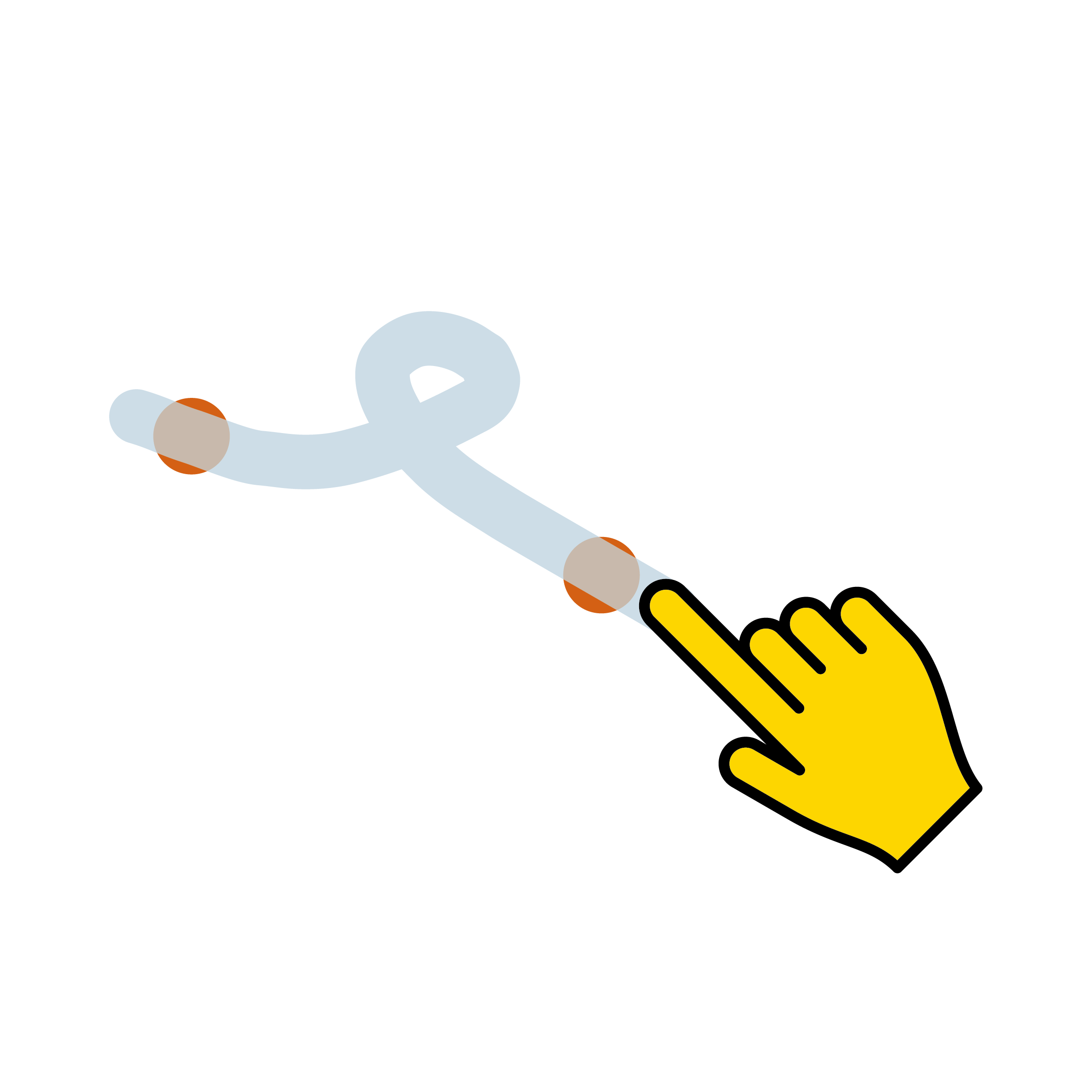
Aby znaleźć środek okręgu opisanego na trójkącie, należałoby wykonać tę konstrukcję na co najmniej dwóch bokach trójkąta. Jest to dość czasochłonne i może szybko stać się nieco zagmatwane. Dlatego użyj dwóch gestów sketchometry Punkt środkowy i Linia prostopadła.
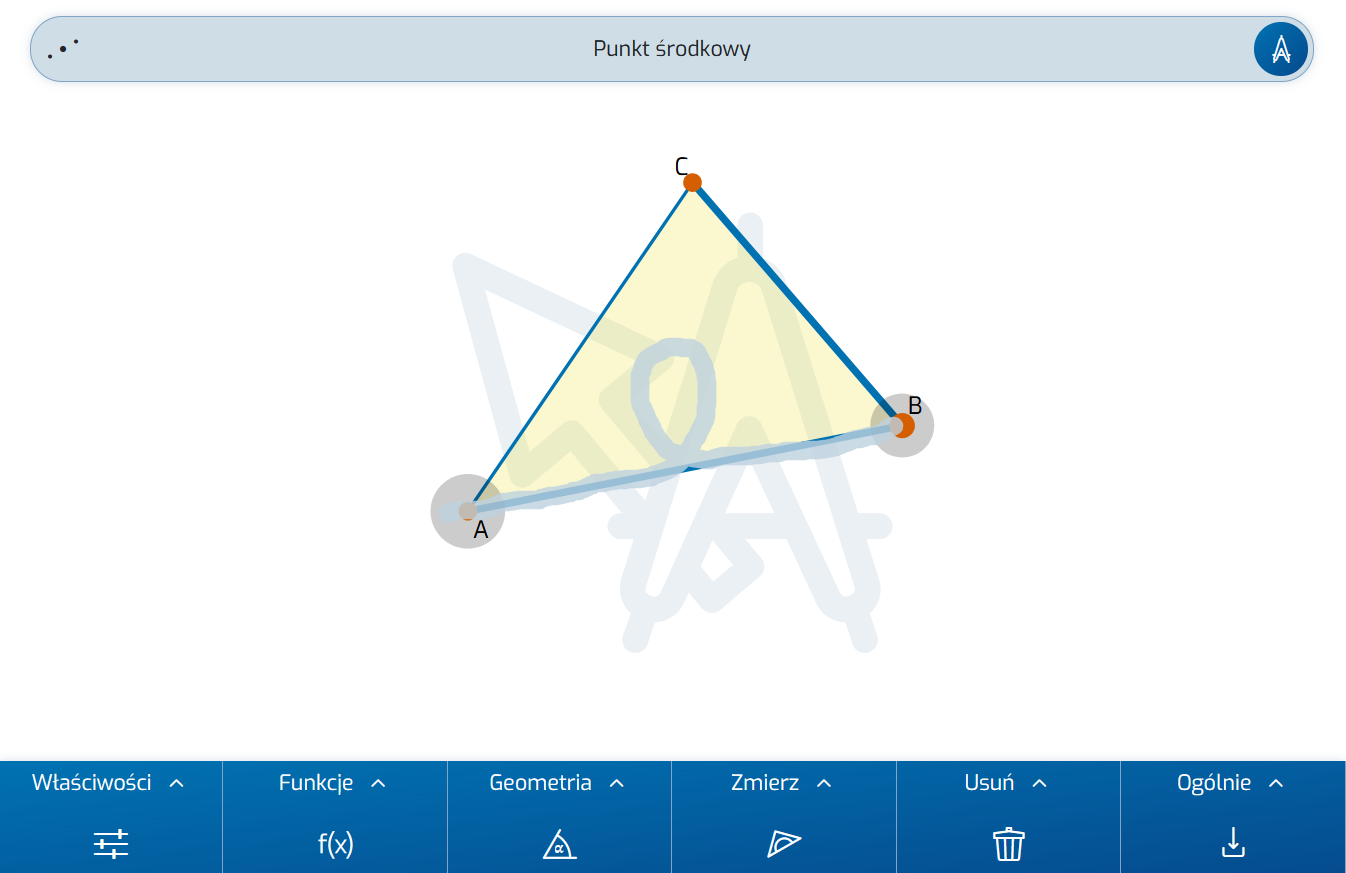
Utwórz trójkąt na nowej tablicy, a następnie punkt środkowy boku trójkąta. Gest Punkt środkowy wygląda jak pętla. Podczas szkicowania gestu zaznacz dwa punkty końcowe wybranego boku trójkąta.
Teraz narysuj linię prostopadłą do boku trójkąta przechodzącą przez jego środek (symetralna boku). Oczywiście ponownie za pomocą gestu.
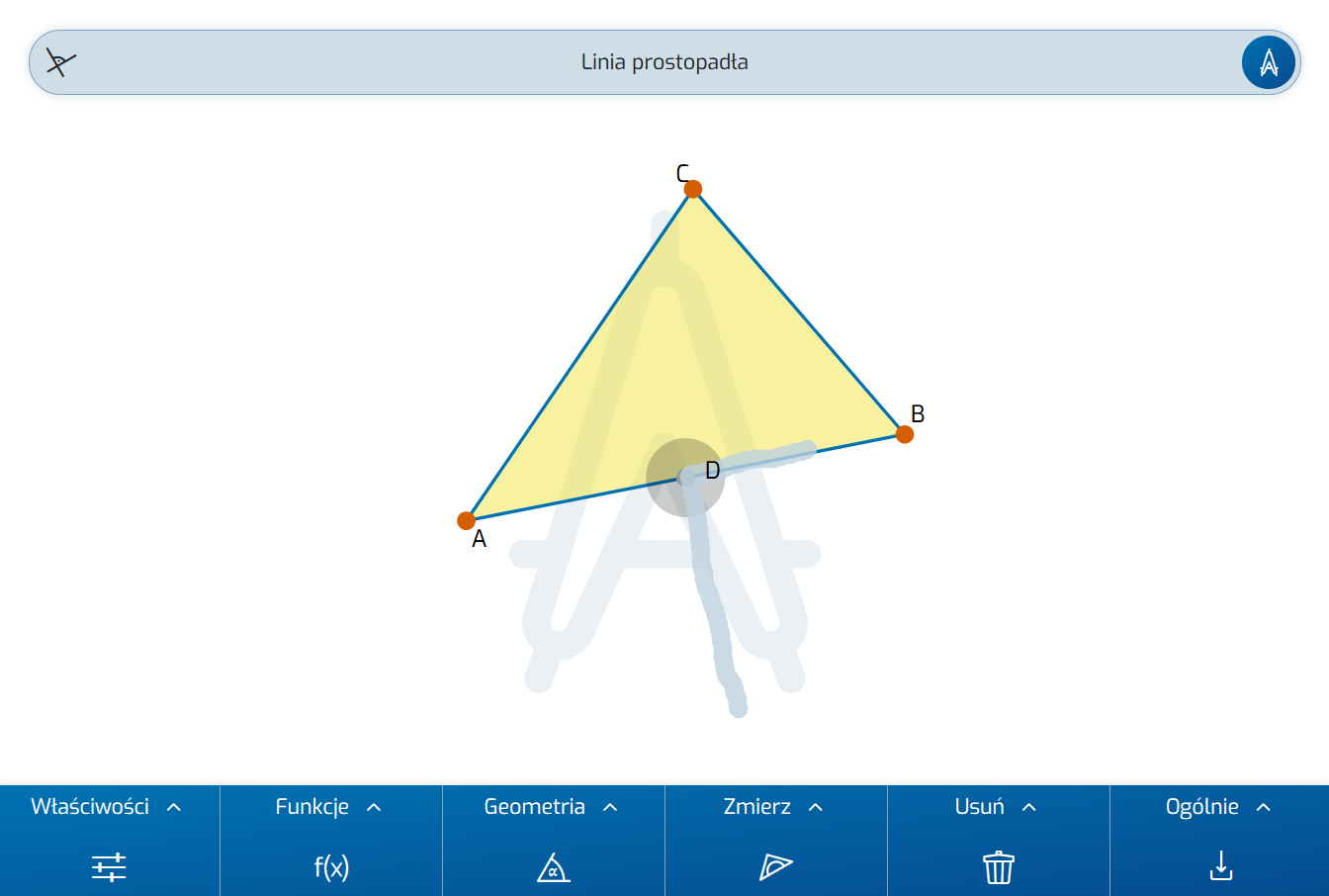
Aby to zrobić, narysuj kąt prosty. Podczas rysowania gestu upewnij się, że zaznaczono punkt środkowy na zgięciu gestu (szary pierścień).
Powtórz te dwa kroki dla pozostałych dwóch boków trójkąta.
Ta procedura jest znacznie szybsza i bardziej przejrzysta niż budowa krok po kroku. Istnieje jednak jeszcze prostszy sposób:
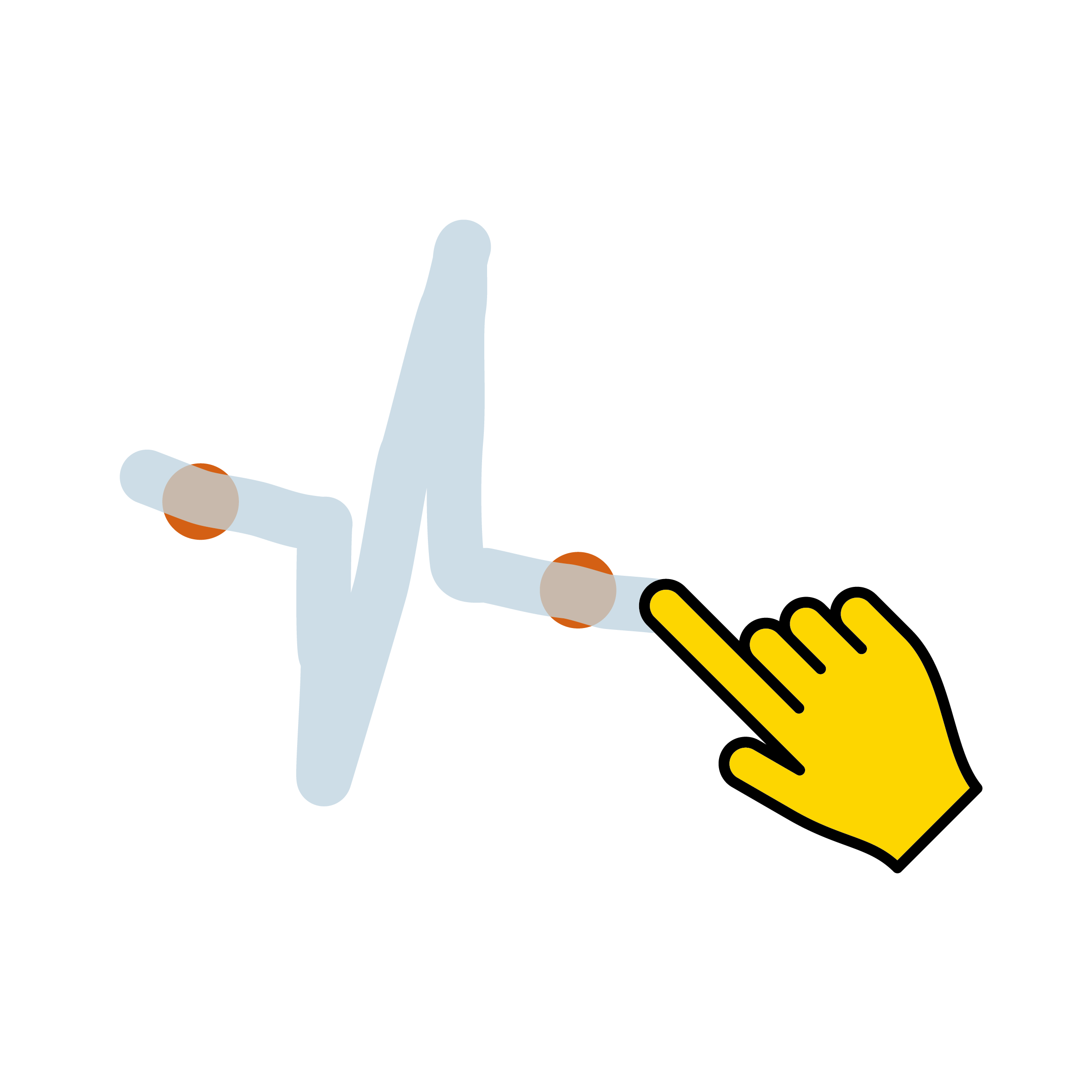
Zamiast gestów Punkt środkowy i Linia prostopadła użyj gestu Symetralna, jak pokazano na rysunku.
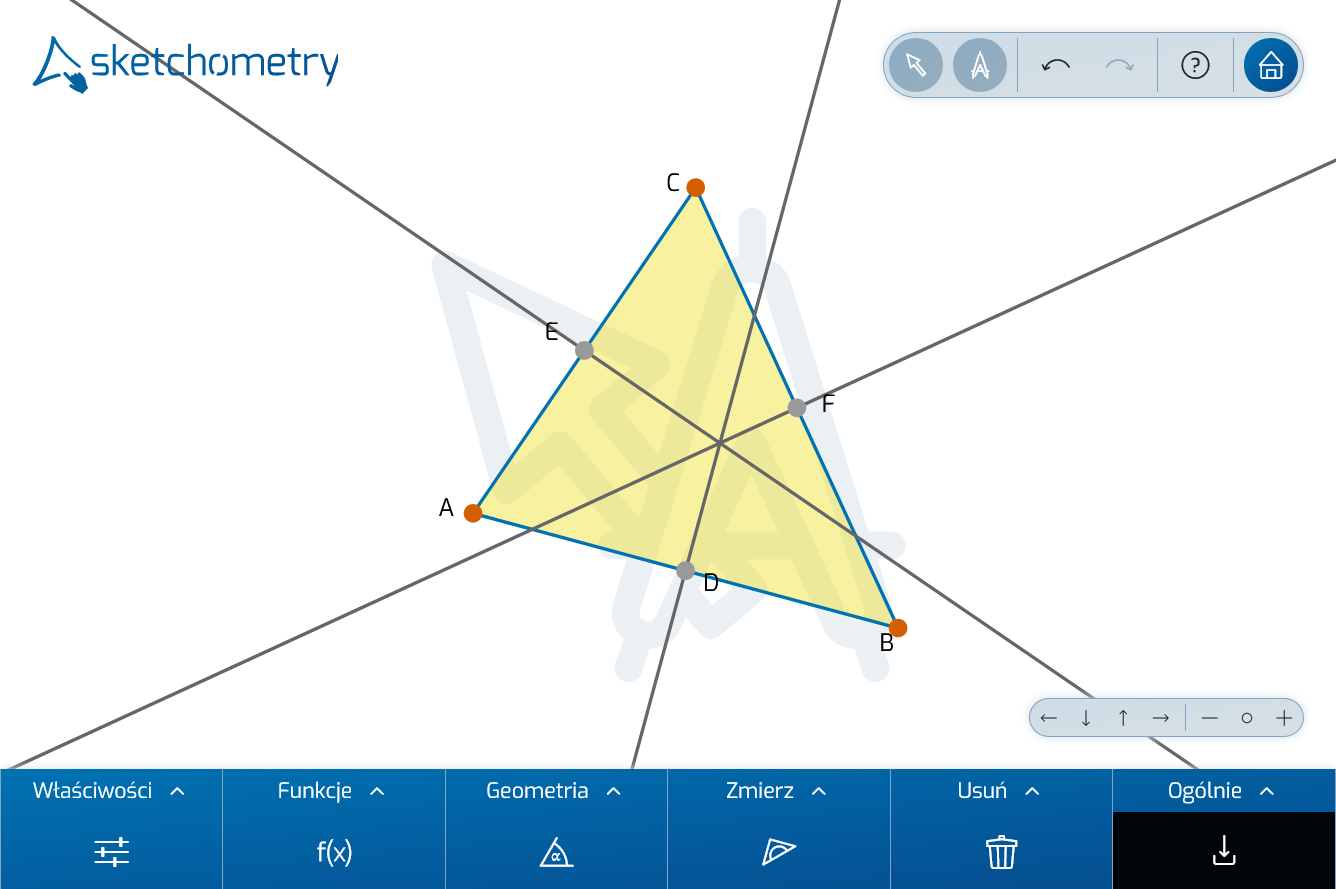
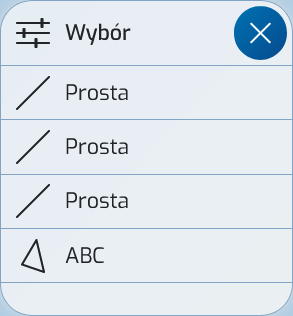
Trzy symetralne boków trójkąta przecinają się w jednym punkcie. Aktywuj Przeciąganie i zmień położenie wierzchołków trójkąta. Wyjaśnienie właściwości przecięcia powinno zostać omówione na zajęciach. Na koniec należy utworzyć punkt środkowy i okrąg opisany. Stuknij w przecięcie prostopadłych linii. Sketchometry może wyświetlić listę wyboru z opcjami przecięcia. Aby zakończyć, narysuj okrąg opisany za pomocą gestu Okrąg (promień).
Teraz konstrukcja jest ukończona. W zależności od wcześniejszej wiedzy uczniów można wybrać odpowiednią opcję konstrukcji: albo podejście krok po kroku, albo gotowe narzędzie gestu.
Zmiana perspektywy:
Następny przykład dotyczy okręgu wpisanego. W klasie można zadać następujące pytanie:
Uczniowie mogą zbadać to pytanie, stosując następującą procedurę: Narysuj trójkąt i okrąg. Dwoma palcami ustaw okrąg tak, aby dotykał trzech boków trójkąta.
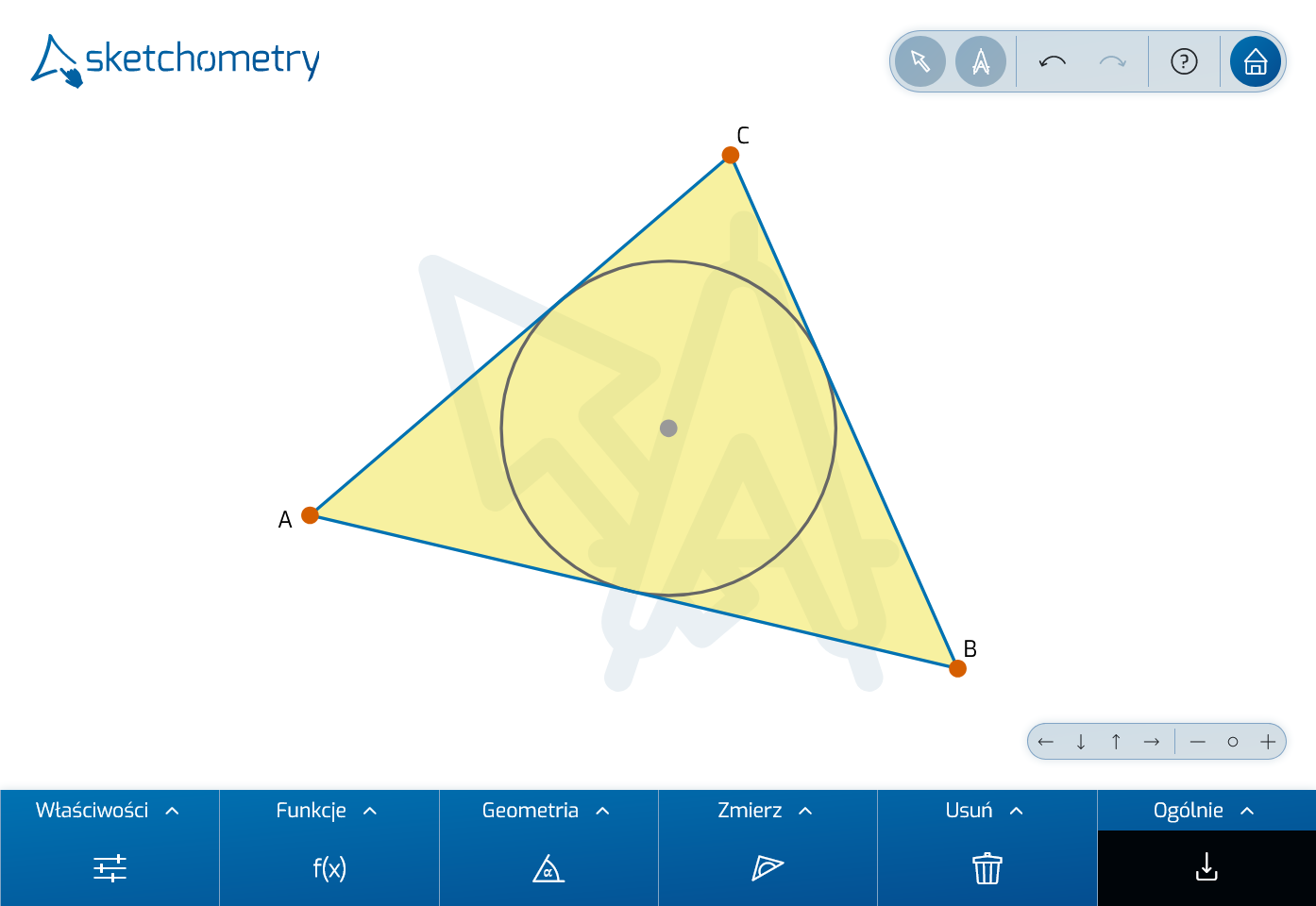
Oczywiście, to nie jest konstrukcja. Tutaj sketchometry jest ponownie używane jako narzędzie do szkicowania: zmień kształt trójkąta i zmień położenie okręgu. Założenie: Zawsze będzie okrąg, który ma pożądaną właściwość. Konstrukcja okręgu wpisanego jest teraz rozwijana krok po kroku.
Na nowej planszy najpierw rozważ dwie przecinające się proste i zaznacz punkt przecięcia. Narysuj okręgi o różnych promieniach i ustaw je tak, aby dotykały obu prostych:
Środki okręgów są równoodległe od dwóch linii prostych (promień!). Narysuj linię prostą, która przebiega przez przecięcie tych dwóch linii i jeden ze środków okręgu.
Możliwe polecenia robocze:
 Biorąc pod uwagę powyższe rozważania, znaczenie dwusiecznej kąta dla konstrukcji okręgu wpisanego staje się jasne.
Biorąc pod uwagę powyższe rozważania, znaczenie dwusiecznej kąta dla konstrukcji okręgu wpisanego staje się jasne.
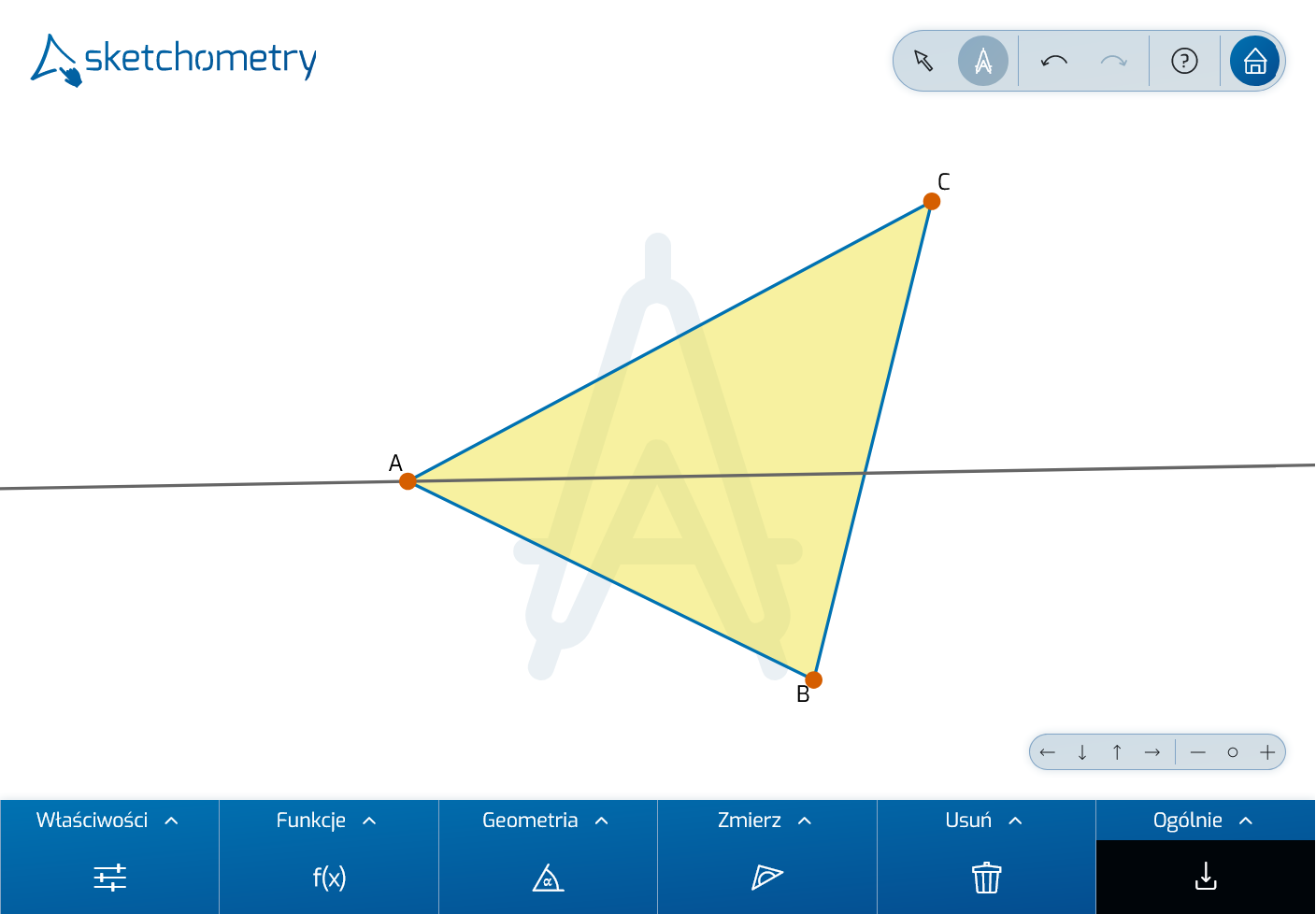
Otwórz nową planszę i dezaktywuj Przeciąganie. Aby ułatwić konstruowanie okręgu wpisanego w trójkąt, istnieje prosty gest tworzenia dwusiecznej kąta. Wygląda to jak litera W.
Zgodnie z mottem „blisko obiektu”, podczas rysowania gestu najpierw zaznacz pierwsze ramię kąta, następnie sektor, w którym leży dwusieczna kąta, a na końcu drugie ramię:
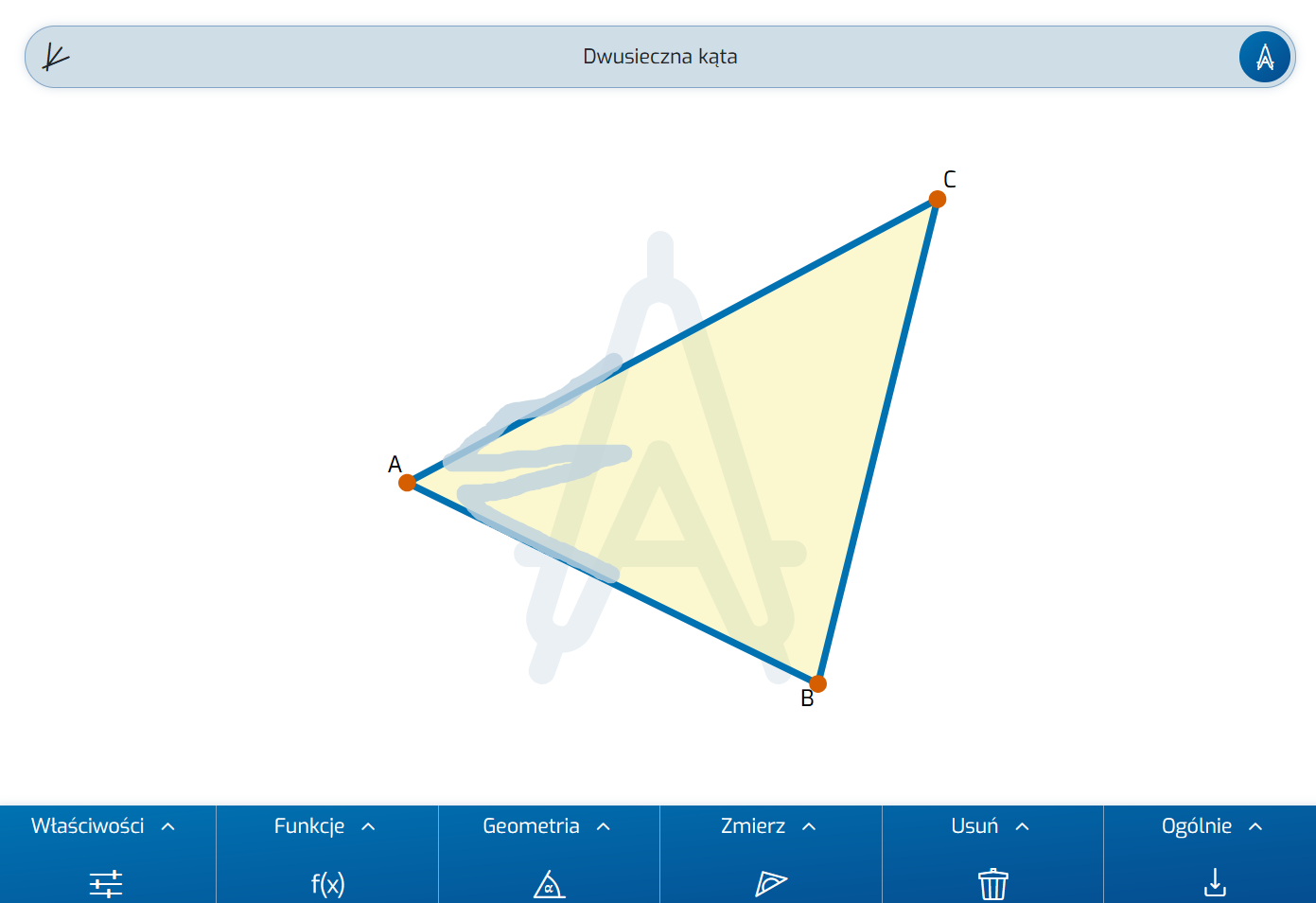
Dodaj dwusieczne pozostałych dwóch kątów. Podobnie jak w przypadku symetralnych boków, można wykazać, że dwusieczne kątów przecinają się w jednym punkcie. Zaznacz ten punkt przecięcia. Znajduje się on w tej samej odległości od wszystkich boków trójkąta.
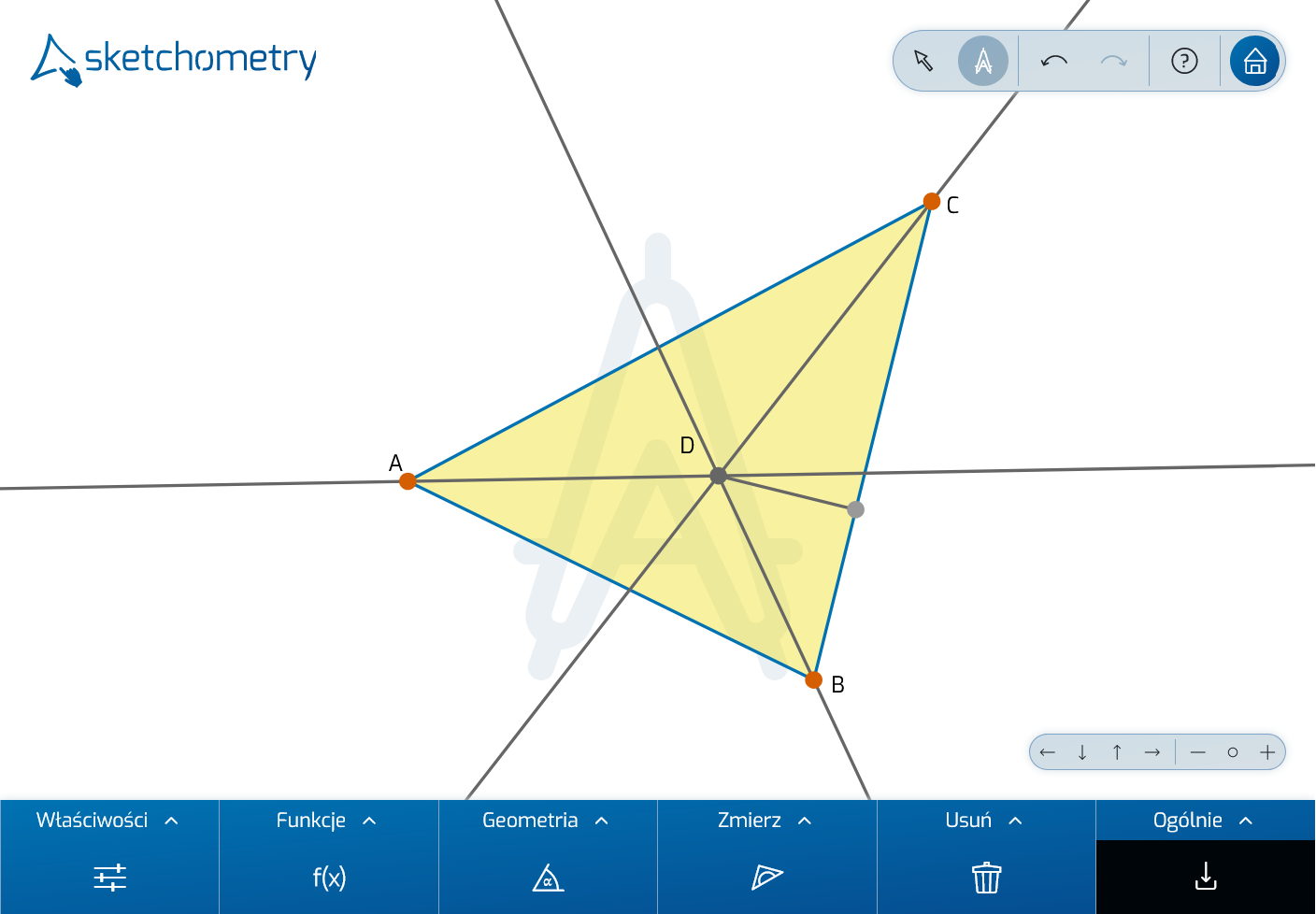
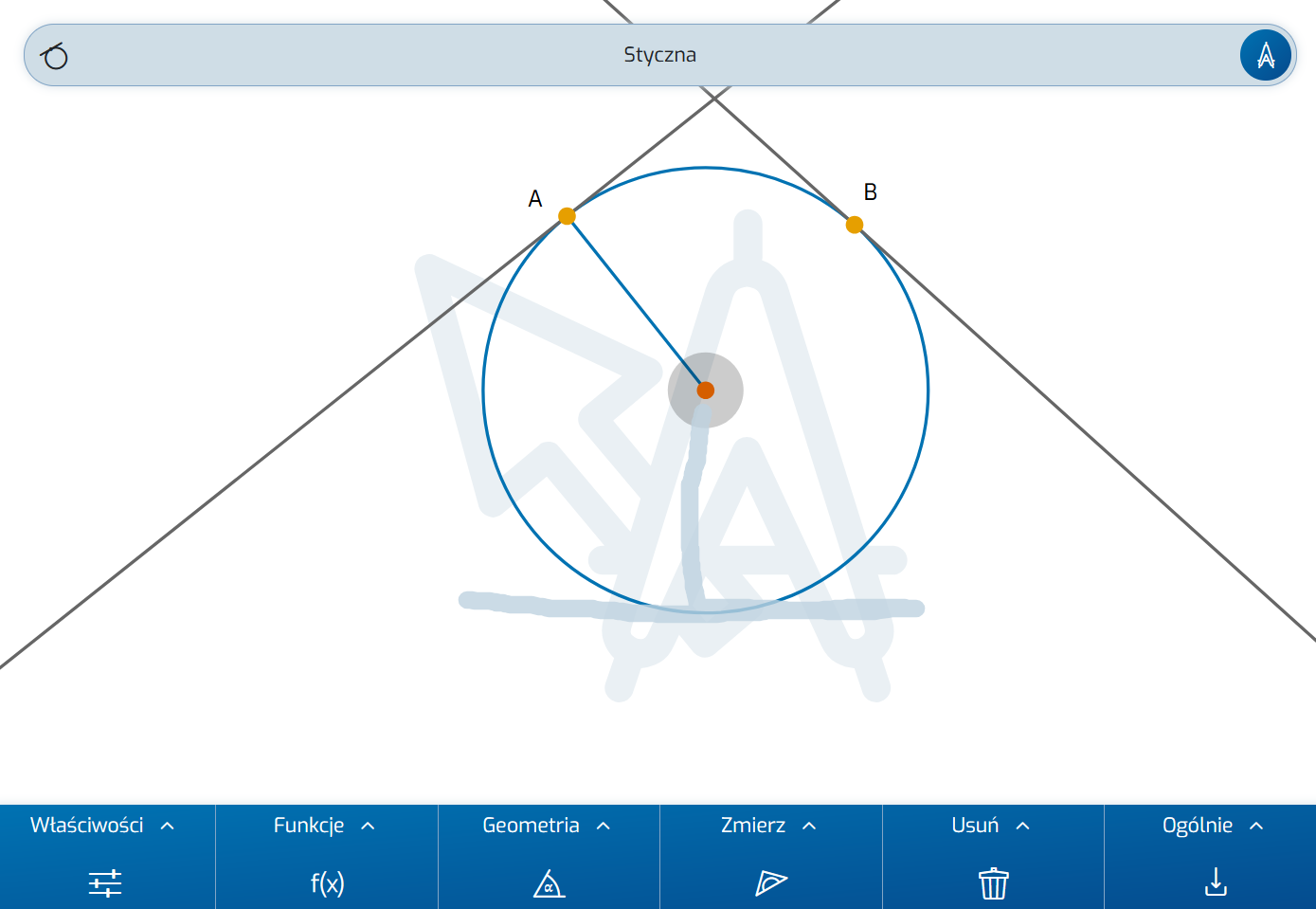
Do narysowania okręgu wpisanego potrzebny jest jeszcze promień. Aby to uzyskać, użyj znanego gestu prostopadłej z niewielką zmianą:
należy rozpocząć gest bezpośrednio w punkcie przecięcia dwusiecznych, a nie przed nim. Oprócz odcinka prostopadłego, sketchometry tworzy również odpowiedni punkt odcinka prostopadłego na okręgu.
Użyj gestu Okrąg (promień), aby utworzyć okrąg wpisany i konstrukcja jest zakończona.
Okrąg wpisany dotyka wszystkich trzech boków danego trójkąta. Dany jest okrąg i szukamy trójkąta, którego boki stykają się z tym okręgiem?
Narysuj okrąg na nowej planszy. Ponieważ boki trójkąta mają dotykać okręgu, muszą być styczne do okręgu. Teraz rozważmy dwie opcje:
W przypadku pierwszej opcji znasz już wszystkie niezbędne gesty:
Druga opcja z gestem jest o wiele bardziej elegancka: Teraz naszkicuj wielką literę T na linii okręgu. Kształt litery T wskazuje kierunek stycznej, a także kierunek promienia.
Teraz naszkicuj wielką literę T na linii okręgu. Kształt litery T wskazuje kierunek stycznej, a także kierunek promienia.
Gest jest łatwy do zapamiętania. Działa on również w przypadku wykresów funkcji i krzywych. Wraz ze styczną, sketchometry tworzy również punkt styczności jako punkt ślizgający. Po dodaniu trzech stycznych do okręgu zaznacz punkty ich przecięcia. Na koniec narysuj trójkąt, którego wierzchołkami będą te trzy punkty przecięcia, aby zaznaczyć obszar trójkąta.
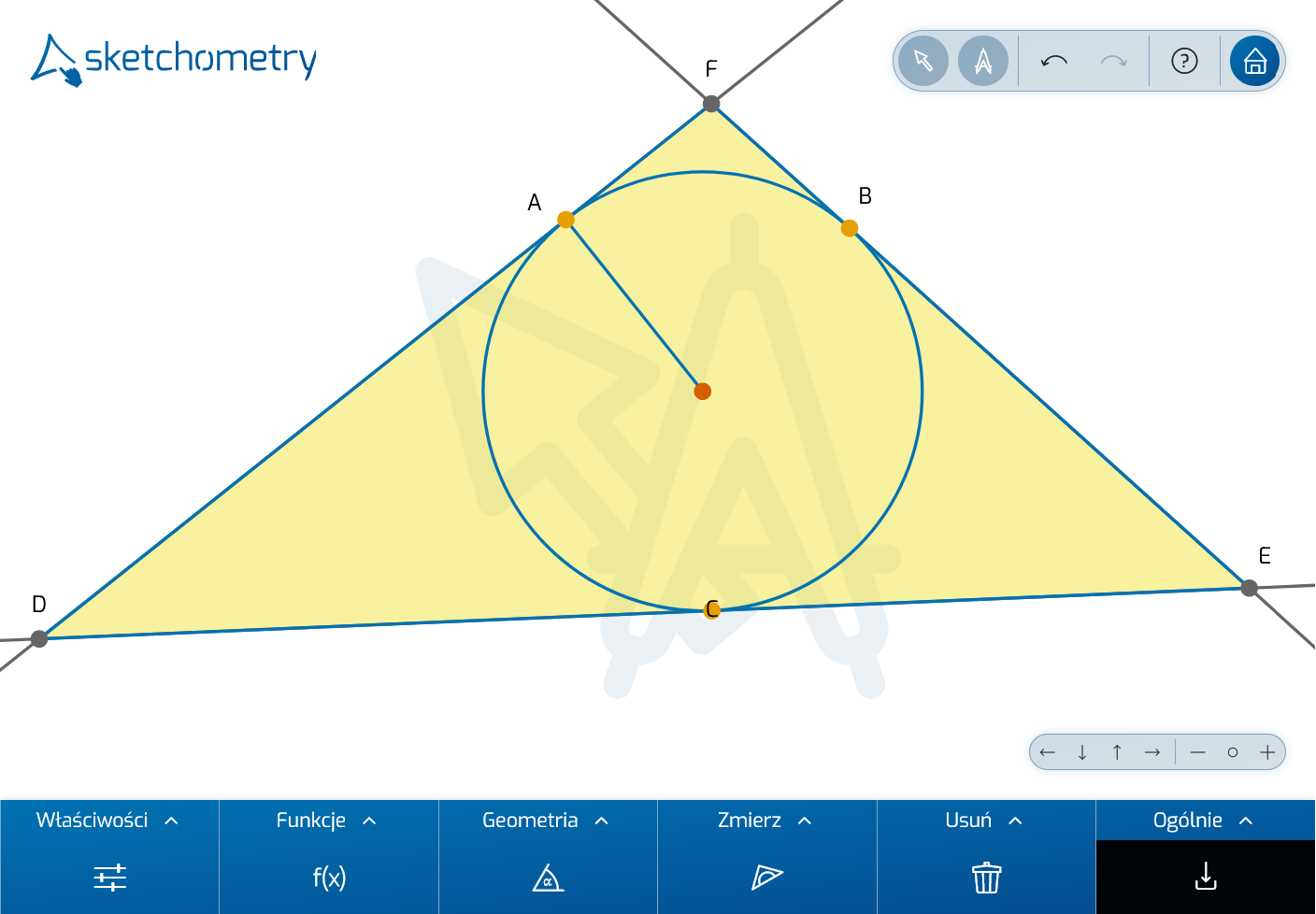
Pierwotny okrąg jest teraz okręgiem wpisanym w trójkąt. Zmień położenie punktów i obserwuj konstrukcję.
Teraz ustaw trzy punkty ślizgające się (punkty styczności) tak, aby znajdowały się tylko w jednej połówce okręgu:
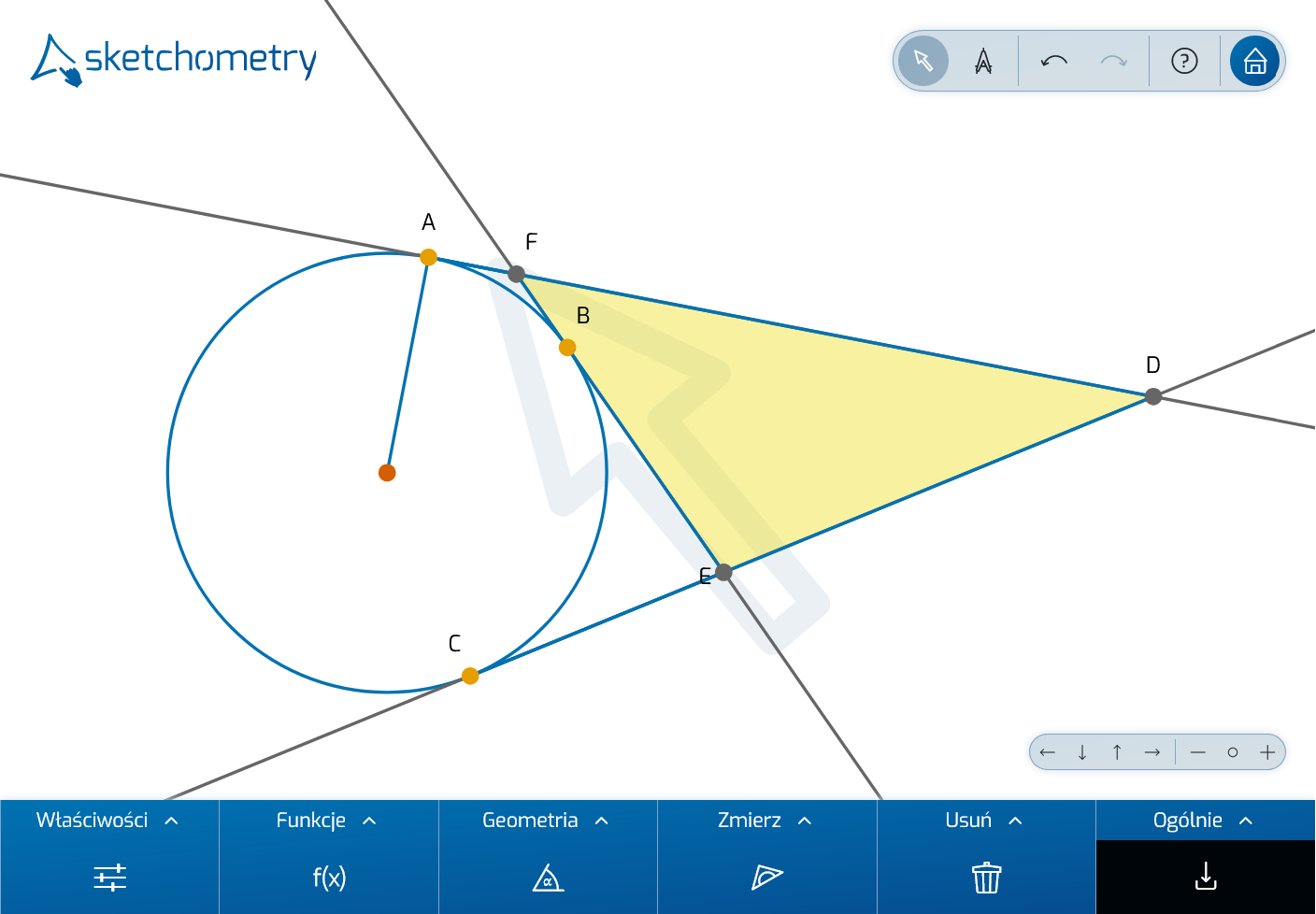
Co się dzieje? A przede wszystkim, dlaczego? Powstaje tzw. okrąg dopisany do trójkąta, co prowadzi do dalszych pytań:

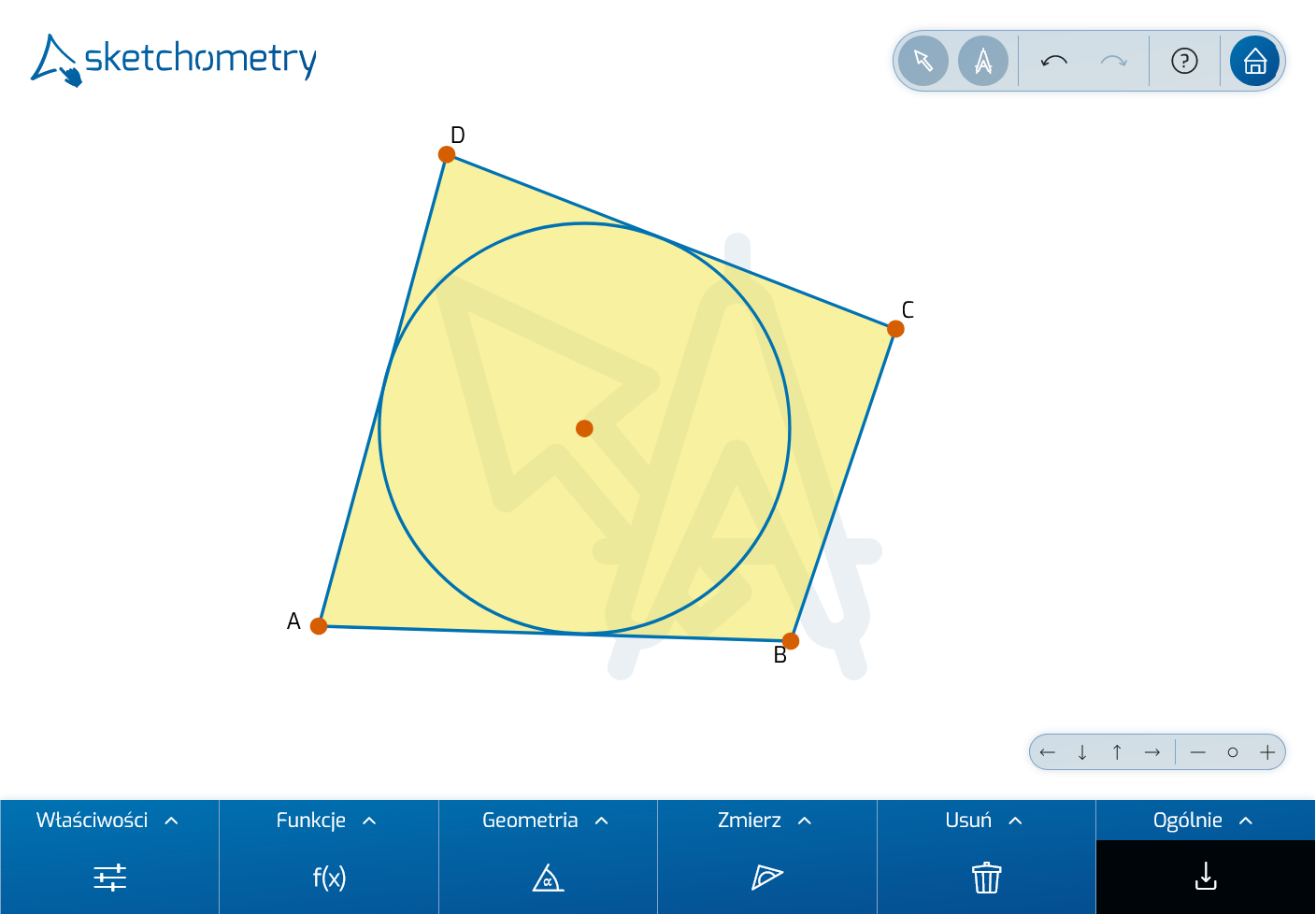
Teraz narysuj cztery styczne do okręgu zamiast trzech. Użyj punktów przecięcia stycznych, aby utworzyć czworokąt, tzw. czworokąt opisany na okręgu.
Tutaj również zmień punkt widzenia. Naszkicuj czworokąt na nowej tablicy, narysuj dodatkowy okrąg i spróbuj umieścić go tak, aby dotykał wszystkich czterech boków czworokąta. W porównaniu do trójkąta, nie zawsze istnieje rozwiązanie. Dlatego warto również przeanalizować różne kształty czworokątów.
Okrąg musi być wielokrotnie przemieszczany. Uczniowie omawiają swoje obserwacje. Tutaj używają sketchometry jako narzędzia do szkicowania.
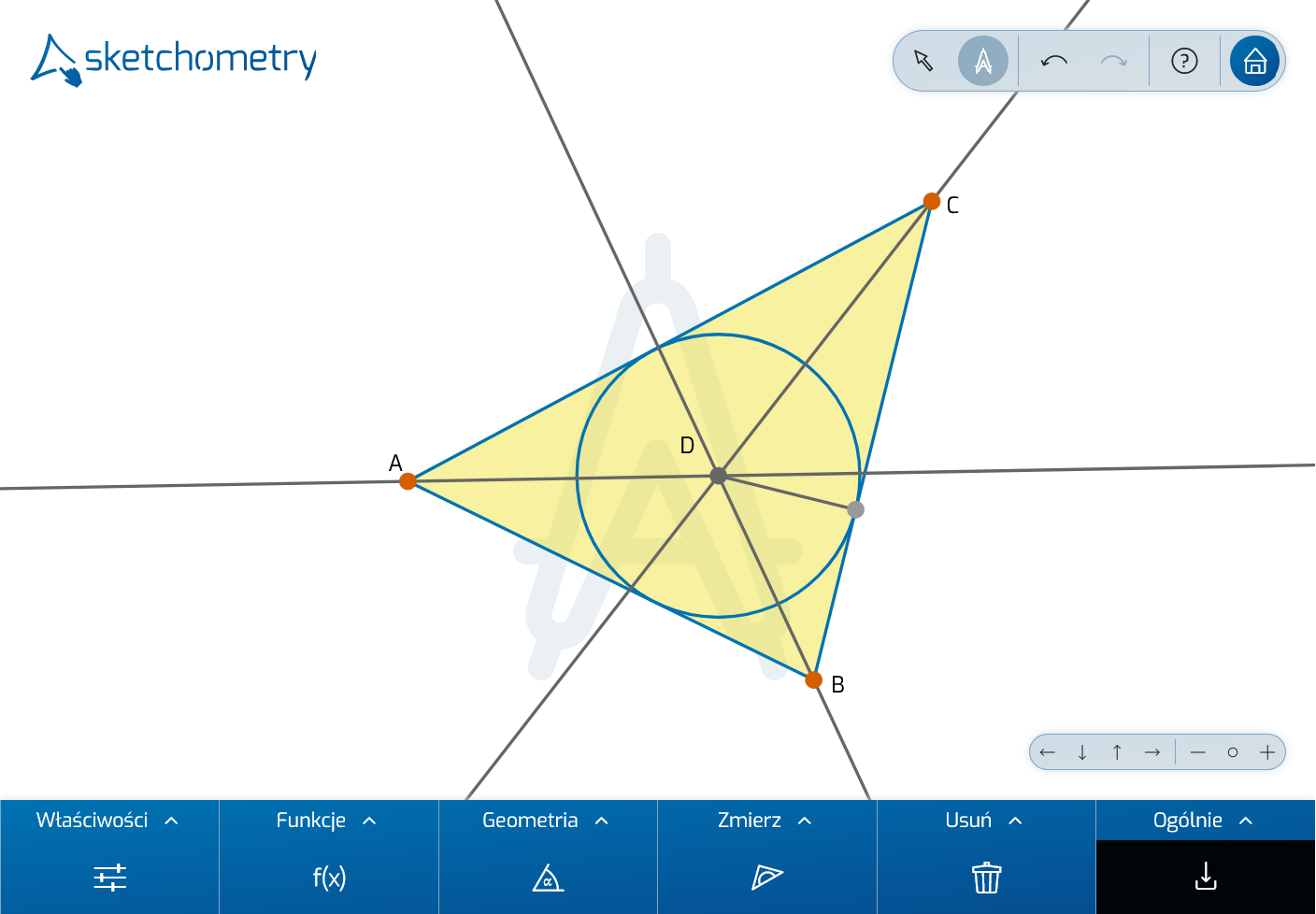
Oprócz licznych gestów, sketchometry oferuje również różne narzędzia pomiarowe: narysuj trójkąt i zaznacz jego kąty wewnętrzne. Jak?
W ten sam sposób, jak na tablicy: naszkicuj łuk od pierwszego ramienia kąta do drugiego ramienia. Zwróć uwagę, że sketchometry zawsze odlicza kąty przeciwnie do ruchu wskazówek zegara. Dodaj również pozostałe dwa kąty wewnętrzne:

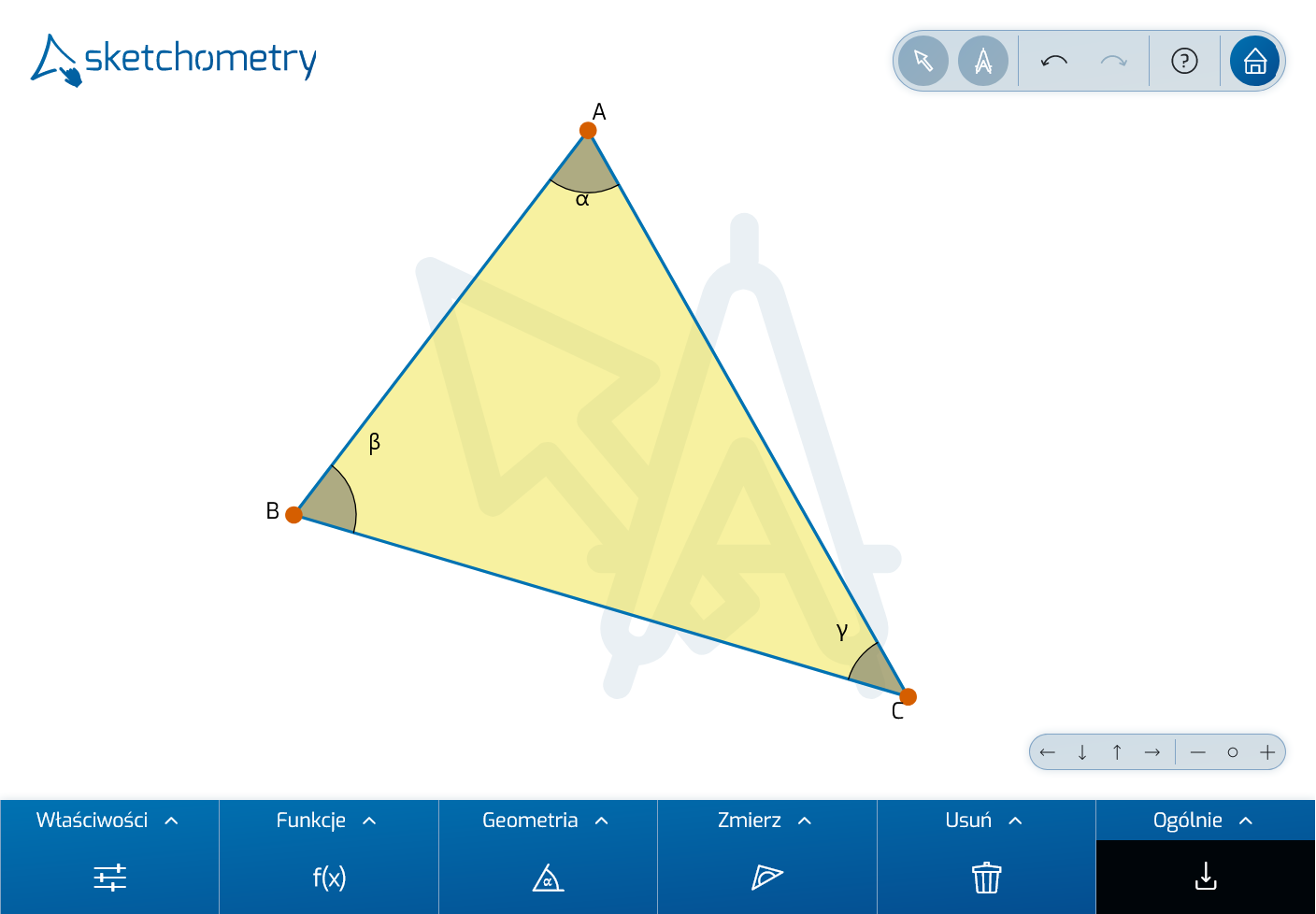
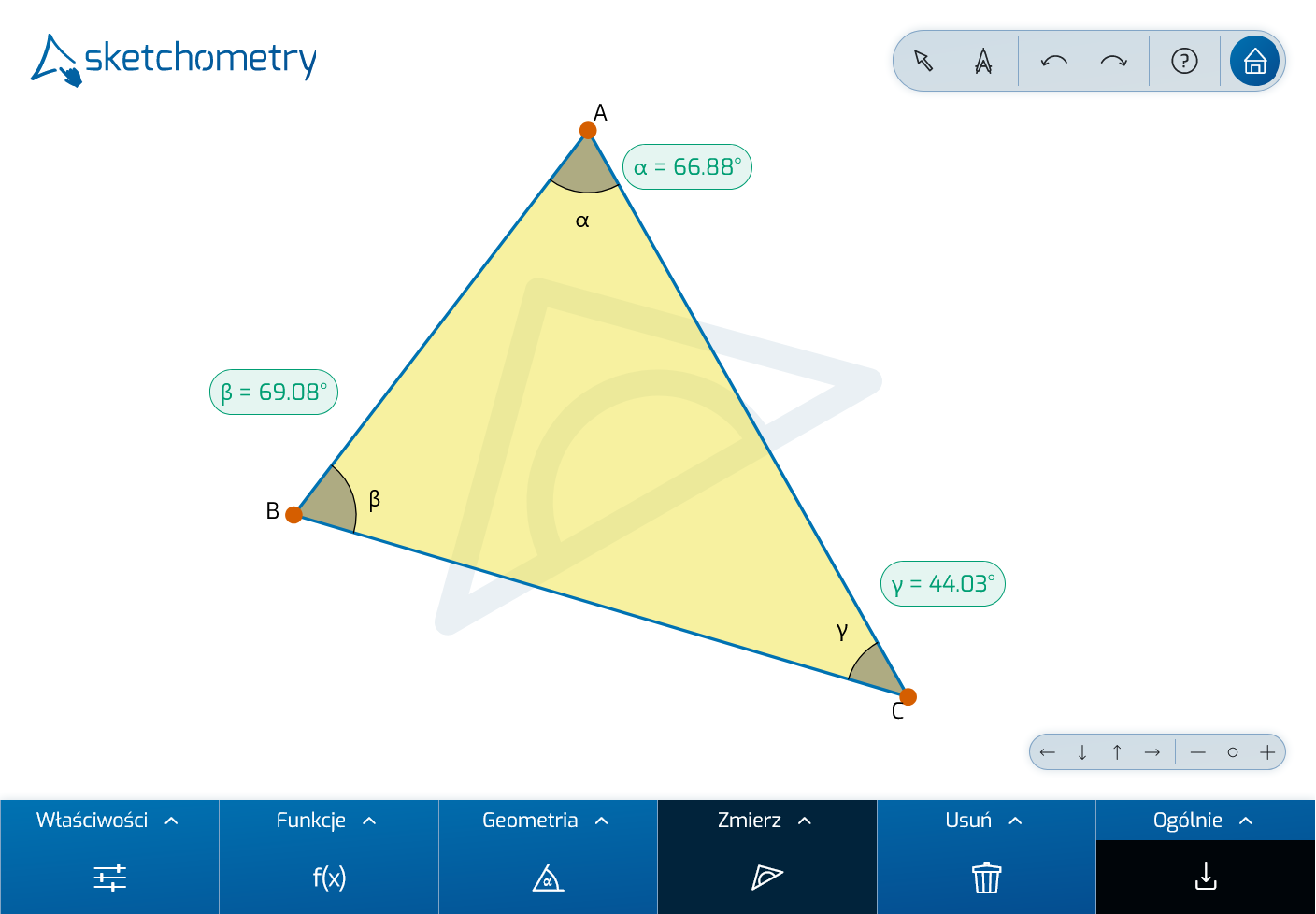
Po utworzeniu obiektu kątowego można określić jego miarę. Aby to zrobić, aktywuj narzędzie  Zmierz na pasku narzędzi.
Zmierz na pasku narzędzi.
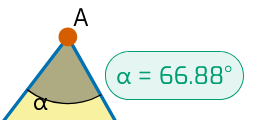 Stuknij w kąt, aby wyświetlić pomiar. Dopóki funkcja
Stuknij w kąt, aby wyświetlić pomiar. Dopóki funkcja  Zmierz jest aktywna, można dodawać kolejne obiekty pomiarowe, a także przeciągać je (bez konieczności przełączania się na funkcję Przeciąganie).
Zmierz jest aktywna, można dodawać kolejne obiekty pomiarowe, a także przeciągać je (bez konieczności przełączania się na funkcję Przeciąganie).
Gdy tylko mierzony obiekt zostanie zmodyfikowany, wynik zostanie automatycznie dostosowany. Sketchometry otwiera okno listy, jeśli istnieje kilka obiektów, które można zmierzyć w miejscu dotknięcia. Długości i powierzchnie są mierzone w ten sam sposób:
 Zmierz.
Zmierz.Oprócz funkcji  Zmierz, sketchometry umożliwia także wykonywanie obliczeń:
Zmierz, sketchometry umożliwia także wykonywanie obliczeń:
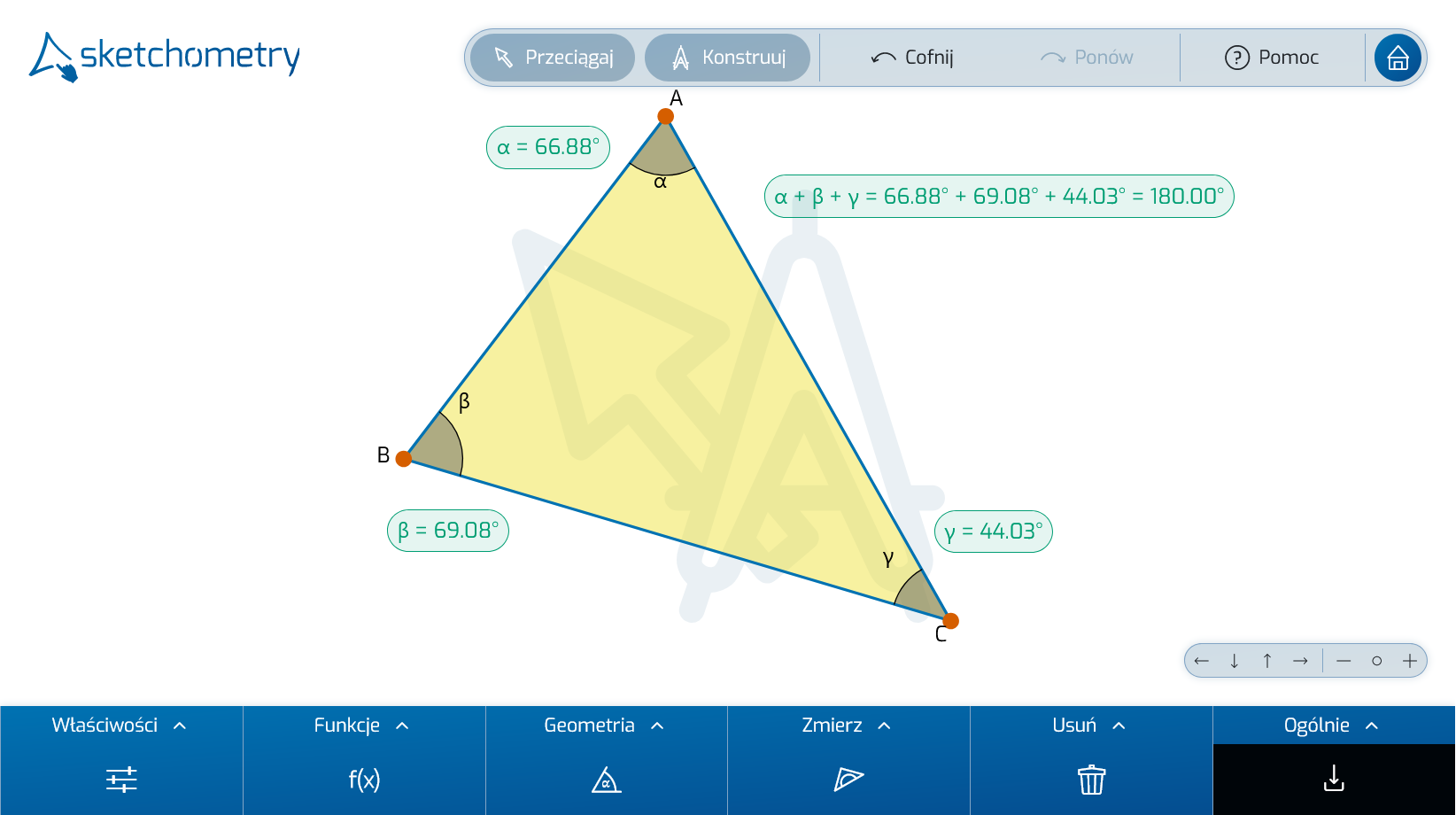
 Suma
Suma Różnica
Różnica Iloczyn
Iloczyn Iloraz
IlorazW powyższym przykładzie określ sumę kątów trójkąta. Aby to zrobić, aktywuj  Suma na pasku narzędzi i stuknij kolejno trzy pomiary. Na pasku informacji pojawi się podgląd:
Suma na pasku narzędzi i stuknij kolejno trzy pomiary. Na pasku informacji pojawi się podgląd: 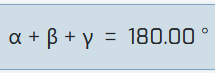 Następnie kliknij wolne miejsce na tablicy. Pojawi się suma pomiarów.
Następnie kliknij wolne miejsce na tablicy. Pojawi się suma pomiarów.
Jednak narzędzia  ,
,  ,
,  i
i  są jeszcze bardziej elastyczne. Na przykład za pomocą narzędzia
są jeszcze bardziej elastyczne. Na przykład za pomocą narzędzia  Iloraz można również klikać bezpośrednio na obiekty i nie trzeba najpierw tworzyć indywidualnych pomiarów, jak pokazuje poniższy przykład:
Iloraz można również klikać bezpośrednio na obiekty i nie trzeba najpierw tworzyć indywidualnych pomiarów, jak pokazuje poniższy przykład:
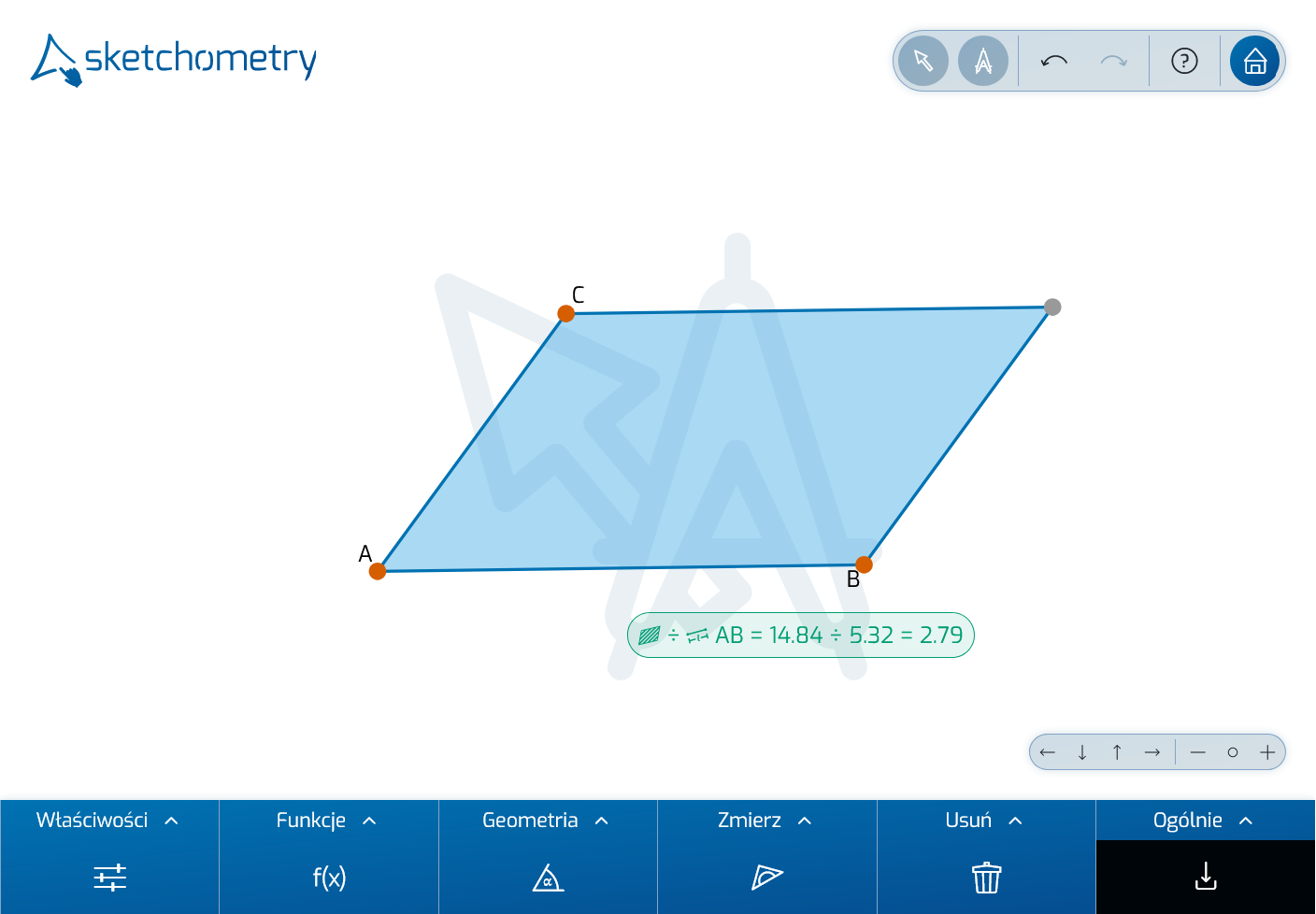
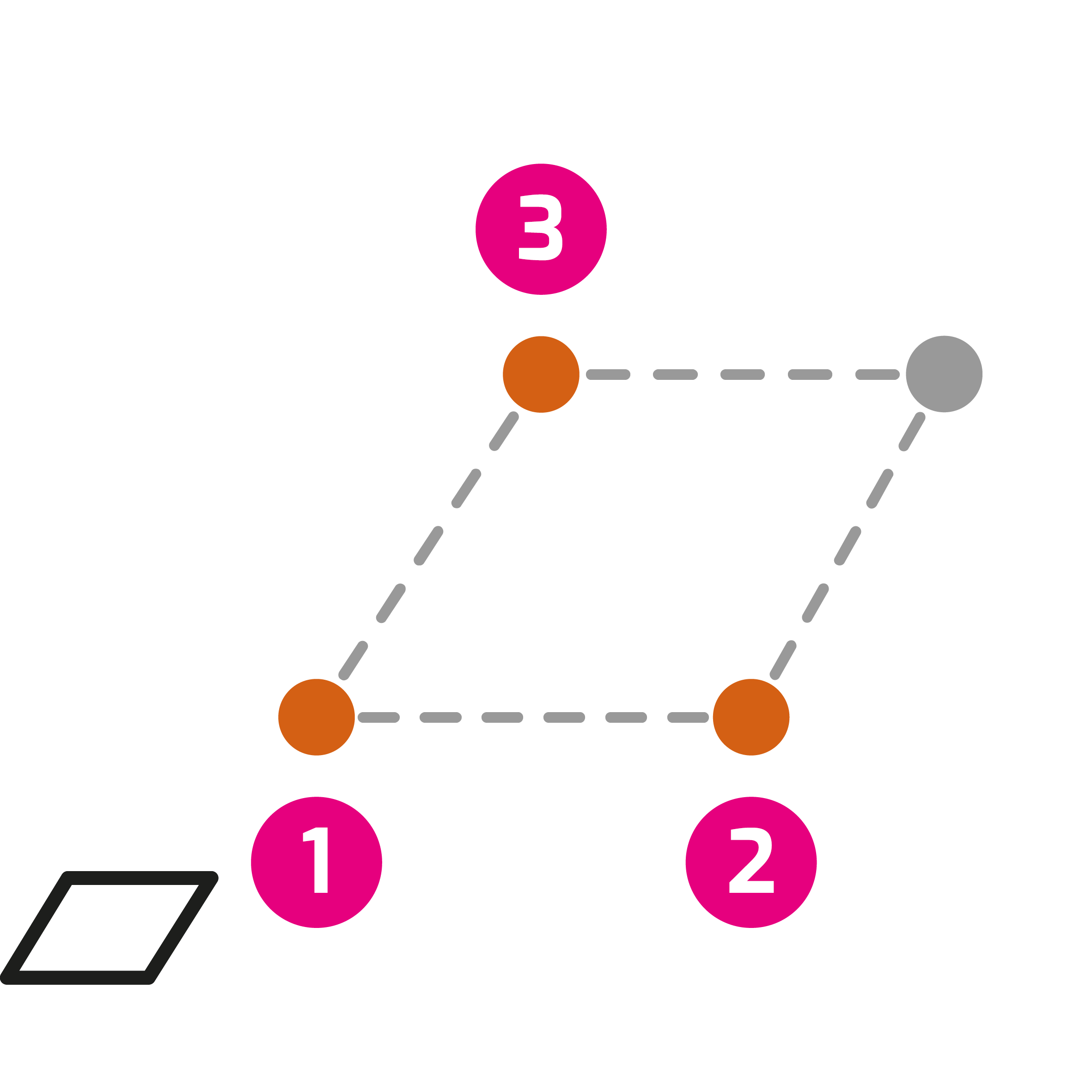 Umieść trzy punkty na nowej planszy, wybierz narzędzie
Umieść trzy punkty na nowej planszy, wybierz narzędzie  Równoległobok i stuknij punkty jeden po drugim. Pojawi się równoległobok. Teraz wybierz narzędzie
Równoległobok i stuknij punkty jeden po drugim. Pojawi się równoległobok. Teraz wybierz narzędzie  Iloraz i dotknij najpierw obszaru równoległoboku (dzielna), a następnie boku (podstawy) równoległoboku (dzielnik). Umieść wynik (= iloraz) na planszy. Wskazuje on długość wysokości równoległoboku.
Iloraz i dotknij najpierw obszaru równoległoboku (dzielna), a następnie boku (podstawy) równoległoboku (dzielnik). Umieść wynik (= iloraz) na planszy. Wskazuje on długość wysokości równoległoboku.
Wreszcie obliczenia mogą być także częścią innych obliczeń.
Warsztaty te zapewniają pierwszy wgląd w pracę z narzędziem szkicowania sketchometry i mają za zadanie ułatwić nauczycielowi wprowadzenie jego funkcjonalności w klasie. Oprócz licznych gestów geometrycznych dostępne są również narzędzia do rachunku różniczkowego i całkowego. Na przykład trójkąt nachylenia można łatwo naszkicować na interaktywnym wykresie funkcji. W miarę oswajania się uczniów z narzędziem warto te bardziej zaawansowane funkcje sygnalizować. Przegląd gestów przydatny w klasie jest dostępny z poziomu samego narzędzia, na pasku Menu, pod znakiem zapytania. Nieco bardziej rozbudowany, z możliwością wyświetlania w dużym formacie - przydatny dla naczyciela podczas prezentacji, czy instruowania uczniów w klasie - dostępny pod linkiem na górze strony.
Spis przykładowych scenariuszy i konstrukcji sketchometry dostępnych na portalu edukator.pl
Fascynująco proste. Po prostu fascynujące - to jest motto sketchometry. Zgodnie z nim to intuicyjne narzędzie pozwala dać uczniom maksimum przestrzeni do własnych poszukiwań, odkryć i wyciągania samodzielnych wniosków. Stworzone do uczenia się w oparciu o samodzielne dociekanie (inquiry-based learning), wymaga jedynie dyskretnego nadzoru i ukierunkowania ze strony nauczyciela, zamiast przytłaczających szczegółowych instrukcji i poleceń.
Poniższe przykładowe materiały mają za zadanie jedynie ułatwić nauczycielowi przygotowanie zróżnicowanych scenariuszy zajęć dostosowanych do poziomu klasy czy indywidualnego ucznia lub ułatwić wykorzystanie gotowych kostrukcji podczas wykładu i nie powinny być traktowane jako instrukcja dla ucznia.
Funkcja liniowa
sketchometry
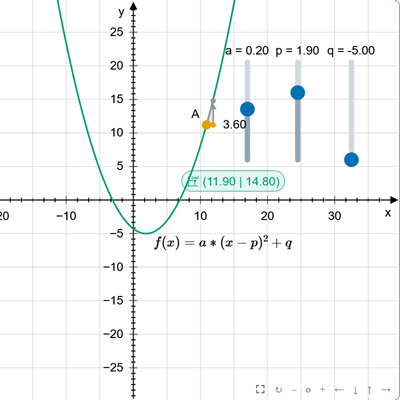
Funkcja kwadratowa - postać kanoniczna
sketchometry
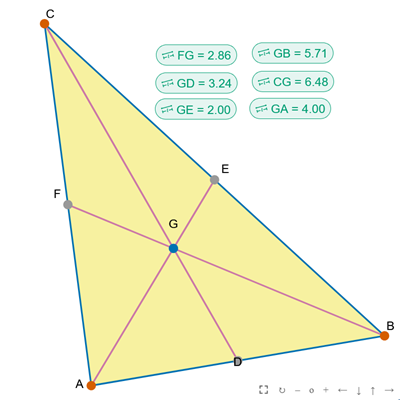
Środek ciężkości trójkąta
sketchometry
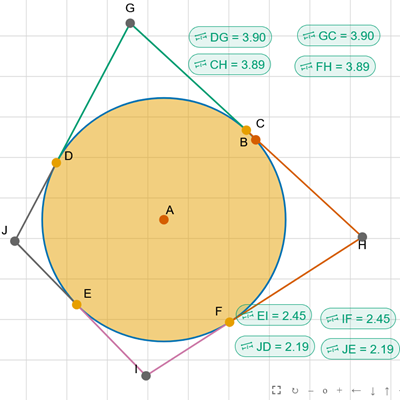
Czworokąt opisany na okręgu
sketchometry
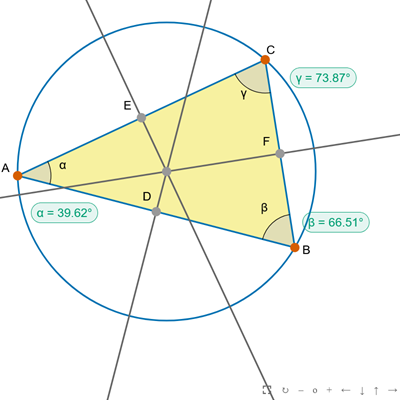
Okrąg opisany na trójkącie
sketchometry
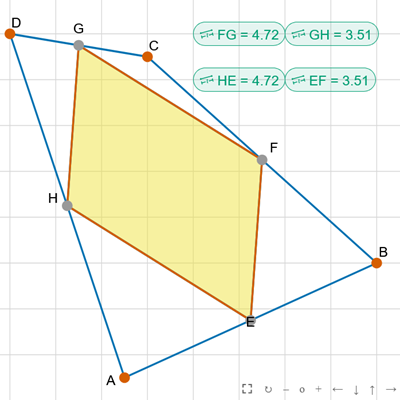
Czworokąt środki
sketchometry
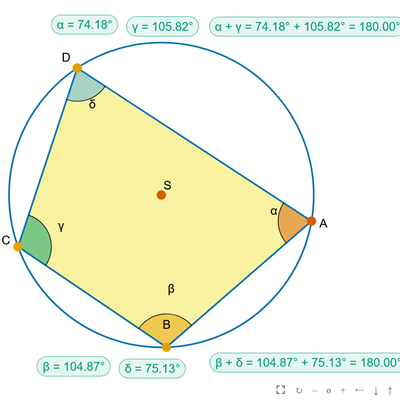
Czworokąt wpisany w okrąg
sketchometry
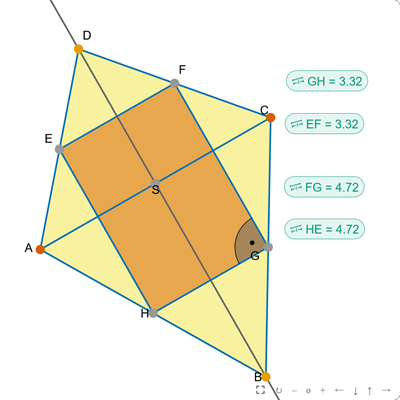
Deltoid środki
sketchometry
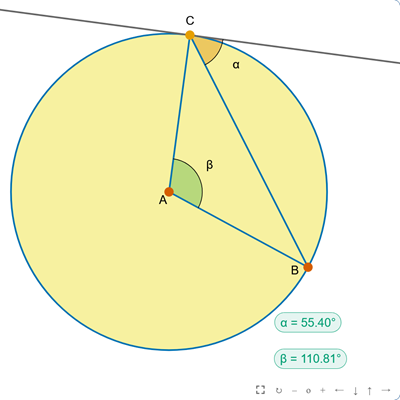
Kąt między styczną i cięciwą
sketchometry
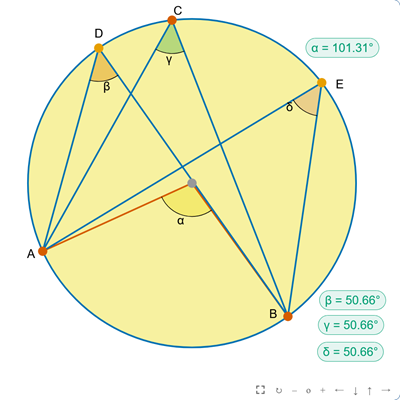
Kąty w okręgu
sketchometry
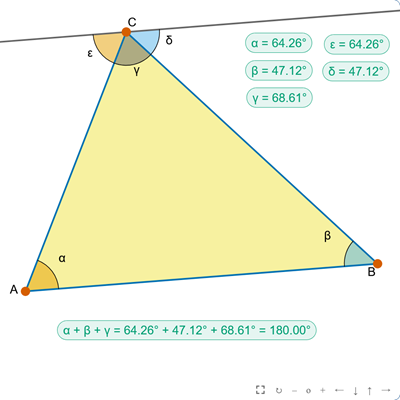
Kąty w trójkącie
sketchometry
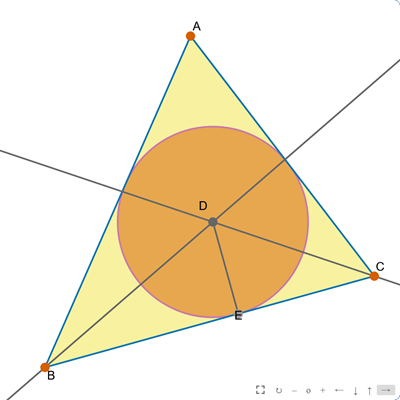
Okrąg wpisany w trójkąt
sketchometry
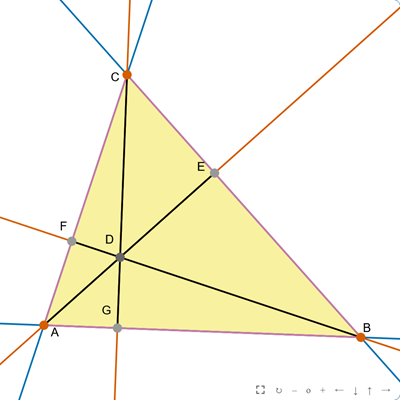
Ortocentrum trójkąta
sketchometry
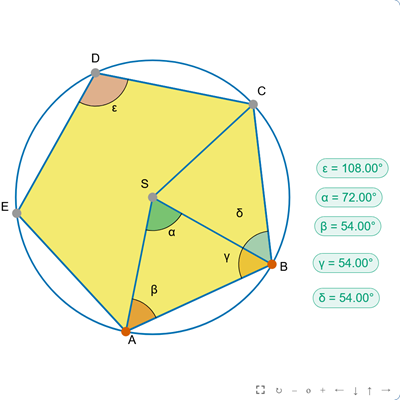
Pięciokąt foremny
sketchometry
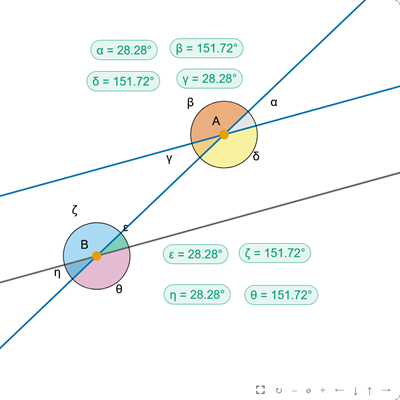
Proste i kąty
sketchometry
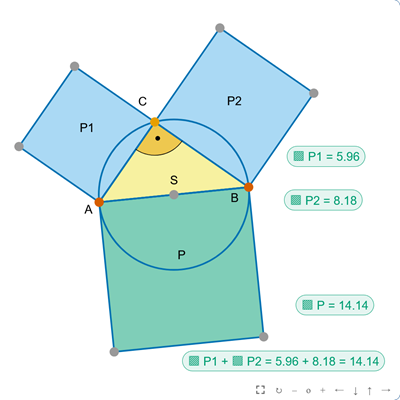
Twierdzenie Pitagorasa
sketchometry
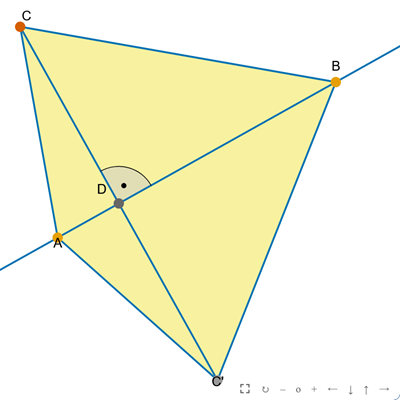
Własności deltoidu
sketchometry
Warunek istnienia trójkąta
sketchometry
Okrąg dopisany do trójkąta
sketchometry
Prosta Gergonne'a
sketchometry